wd wp Пошук: ⬜

Элементарная алгебра

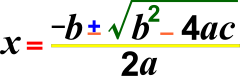
Двухмерны графік (чырвоная крывая) алгебраічнага ўраўнення $\{\displaystyle y=x^\{2\}-x-2\}$

Элемента́рная а́лгебра — самы стары раздзел алгебры, у якім вывучаюцца алгебраічныя выразы і ўраўненні над рэчаіснымі і камплекснымі лікамі.

Асноўныя паняцці

Гл. таксама: Матэматычныя абазначэнні У алгебры прынята запісваць матэматычныя выразы (формулы) у самым агульным выглядзе, замяняючы канкрэтныя лікі на літарныя сімвалы, дзякуючы чаму пры рашэнні аднатыпных задач дасягаецца максімальная агульнасць выніку. Асноўным зместам алгебры з’яўляюцца правілы тоесных пераўтварэнняў формул, неабходныя для рашэння ўраўненняў, аналізу залежнасцей, аптымізацыі разглядаемай сістэмы і іншых практычных задач[1].

Акрамя літар і лікаў, у формулах элементарнай алгебры выкарыстоўваюцца арыфметычныя аперацыі: (складанне, адніманне, множанне, дзяленне, узвядзенне ў ступень, здабыванне кораня) і элементарныя функцыі (лагарыфм, трыганаметрычныя функцыі). Дзве формулы, злучаныя знакам роўнасці, называюцца ўраўненнем.

Калі знак аперацыі паміж двума выразамі не пазначаны, маецца на ўвазе множанне:

a b

a ⋅ b ;

2 x

2 ⋅ x ;

π (

)

π ⋅ (

) .

{\displaystyle ab=a\cdot b;\qquad 1{,}2\ x=1{,}2\cdot x;\qquad \pi (a^{2}+b^{2})=\pi \cdot (a^{2}+b^{2}).}

$\{\displaystyle ab=a\cdot b;\qquad 1\{,\}2\ x=1\{,\}2\cdot x;\qquad \pi (a^\{2\}+b^\{2\})=\pi \cdot (a^\{2\}+b^\{2\}).\}$ Прыклад формулы: плошча трохвугольніка

{\displaystyle S}

$\{\displaystyle S\}$ наступным чынам выражаецца цераз даўжыню адной са старон

{\displaystyle a}

$\{\displaystyle a\}$ і даўжыню вышыні

{\displaystyle h}

$\{\displaystyle h\}$ , апушчанай на старану

{\displaystyle a}

$\{\displaystyle a\}$ :

S

1 2

a h .

{\displaystyle S={1 \over 2}ah.}

$\{\displaystyle S=\{1 \over 2\}ah.\}$ Самы просты алгебраічны выраз — гэта адначлен, які складаецца з лікавага множніка, памножанага на адзін ці больш літарных знакаў[2]. Прыклады:

2 x ;

a b

;

w .

{\displaystyle 1{,}2\ x;\qquad {\sqrt {2}}abc^{2};\qquad x^{2}w.}

$\{\displaystyle 1\{,\}2\ x;\qquad \{\sqrt \{2\}\}abc^\{2\};\qquad x^\{2\}w.\}$ Алгебраічныя сумы (гэта значыць сумы і/ці рознасці) адначленаў называюцца мнагачленамі. Выразы, якія маюць від дзелі аднаго мнагачлена на другі, называюцца алгебраічнымі дробамі. Дзеянні з алгебраічнымі дробамі аналагічныя дзеянням са звычайнымі дробамі — разлажэнне лічніка і назоўніка на множнікі, прывядзенне некалькіх дробаў да агульнага назоўніка, скарачэнне лічніка і назоўніка на агульны множнік і пад.

Прыклад Выраз

− 2 x y + c

{\displaystyle 3x^{2}-2xy+c}

$\{\displaystyle 3x^\{2\}-2xy+c\}$ мае наступныя элементы:

1 : ступень, 2 : каэфіцыент, 3 : адначлен (складнік), 4 : аперацыя, 5 : канстанта (пастаянная),

x , y

{\displaystyle x,y}

$\{\displaystyle x,y\}$ : зменныя

Законы элементарнай алгебры

Вылічэнне значэння выразу

Парадак выканання аперацый паказваецца дужкамі. Калі дужак няма, то прыярытэтнасць, у парадку змяншэння, наступная.

Узвядзенне ў ступень.
Вылічэнне функцыі.
Множанне і дзяленне.
Складанне і адніманне.

Прыклады:

(

)

{\displaystyle a^{b^{c}}=a^{(b^{c})}}

$\{\displaystyle a^\{b^\{c\}\}=a^\{(b^\{c\})\}\}$

sin ⁡

= sin ⁡ (

)

{\displaystyle \sin x^{2}=\sin(x^{2})}

$\{\displaystyle \sin x^\{2\}=\sin(x^\{2\})\}$

sin ⁡ a

b

( sin ⁡ a ) + b

{\displaystyle \sin a+b=(\sin a)+b}

$\{\displaystyle \sin a+b=(\sin a)+b\}$

Пры вылічэнні значэння выразу замест літарных знакаў падстаўляюць іх лікавыя значэнні, якія адпавядаюць канкрэтнай задачы. Мноства лікавых значэнняў, пры якіх выраз мае сэнс, называецца вобласцю дапушчальных значэнняў гэтага выразу[3]. Прыклад: для выразу

a + b

a − b

{\displaystyle {\frac {a+b}{a-b}}}

$\{\displaystyle \{\frac \{a+b\}\{a-b\}\}\}$ вобласць дапушчальных значэнняў — усе пары

a , b

{\displaystyle a,b}

$\{\displaystyle a,b\}$ , у якіх

a ≠ b

{\displaystyle a\neq b}

$\{\displaystyle a\neq b\}$ .

Уласцівасці аперацый

Камутатыўнасць (перамяшчальная ўласцівасць) складання:

a + b

b + a .

{\displaystyle a+b=b+a.}

$\{\displaystyle a+b=b+a.\}$

Адніманне — дзеянне, адваротнае складанню.
Адніманне ліку b раўназначнае складанню з лікам, процілеглым b:

a − b

a + ( − b ) .

{\displaystyle a-b=a+(-b).}

$\{\displaystyle a-b=a+(-b).\}$

Камутатыўнасць (перамяшчальная ўласцівасць) множання:

a ⋅ b

b ⋅ a .

{\displaystyle a\cdot b=b\cdot a.}

$\{\displaystyle a\cdot b=b\cdot a.\}$

Дзяленне — дзеянне, адваротнае множанню.
Дзяленне на нуль немагчыма.
Дзяленне на лік b раўназначнае дамнажэнню на лік, адваротны да b:

a b

= a

(

1 b

)

{\displaystyle {a \over b}=a\left({1 \over b}\right).}

$\{\displaystyle \{a \over b\}=a\left(\{1 \over b\}\right).\}$

Узвядзенне ў ступень не камутатыўнае (не перамяшчальнае). Таму ў яго ёсць дзве адваротныя аперацыі: здабыванне кораня і лагарыфмаванне.
- Прыклад: калі
3

x

= 10

{\displaystyle 3^{x}=10}

$\{\displaystyle 3^\{x\}=10\}$ , то

x

log

3

⁡ 10.

{\displaystyle x=\log _{3}10.}

$\{\displaystyle x=\log _\{3\}10.\}$ Калі

x

2

= 10

{\displaystyle x^{2}=10}

$\{\displaystyle x^\{2\}=10\}$ , то

x

10

.

{\displaystyle x={\sqrt {10}}.}

$\{\displaystyle x=\{\sqrt \{10\}\}.\}$
Корань цотнай ступені з адмоўнага ліку не існуе (сярод рэчаісных лікаў). Гл. камплексныя лікі.
Асацыятыўная (спалучальная) уласцівасць складання:

( a + b ) + c

a + ( b + c ) .

{\displaystyle (a+b)+c=a+(b+c).}

$\{\displaystyle (a+b)+c=a+(b+c).\}$

Асацыятыўная (спалучальная) уласцівасць множання:

( a b ) c

a ( b c ) .

{\displaystyle (ab)c=a(bc).}

$\{\displaystyle (ab)c=a(bc).\}$

Дыстрыбутыўная (размеркавальная) уласцівасць для множання:

c ( a + b )

c a + c b .

{\displaystyle c(a+b)=ca+cb.}

$\{\displaystyle c(a+b)=ca+cb.\}$

Дыстрыбутыўная (размеркавальная) уласцівасць для ўзвядзення ў ступень:

( a b

)

{\displaystyle (ab)^{c}=a^{c}b^{c}.}

$\{\displaystyle (ab)^\{c\}=a^\{c\}b^\{c\}.\}$

Складанне паказчыкаў ступені:

b + c

{\displaystyle a^{b}a^{c}=a^{b+c}.}

$\{\displaystyle a^\{b\}a^\{c\}=a^\{b+c\}.\}$

Перамнажэнне паказчыкаў ступені:

(

)

b c

{\displaystyle (a^{b})^{c}=a^{bc}.}

$\{\displaystyle (a^\{b\})^\{c\}=a^\{bc\}.\}$

Уласцівасці роўнасці

Калі

a

{\displaystyle a=b}

$\{\displaystyle a=b\}$ і

b

{\displaystyle b=c}

$\{\displaystyle b=c\}$ , то

a

{\displaystyle a=c}

$\{\displaystyle a=c\}$ (транзітыўнасць роўнасці).

a = a

{\displaystyle a=a}

$\{\displaystyle a=a\}$ (рэфлексіўнасць).

Калі

a

{\displaystyle a=b}

$\{\displaystyle a=b\}$ , то

b

{\displaystyle b=a}

$\{\displaystyle b=a\}$ (сіметрычнасць).

Іншыя законы

Калі

a

{\displaystyle a=b}

$\{\displaystyle a=b\}$ і

c

{\displaystyle c=d}

$\{\displaystyle c=d\}$ , то

a + c

b + d .

{\displaystyle a+c=b+d.}

$\{\displaystyle a+c=b+d.\}$ (адытыўнасць роўнасці) + Калі

a
=
b


\{\displaystyle a=b\}

![\{\displaystyle a=b\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1956b03d1314c7071ac1f45ed7b1e29422dcfcc4), то 



a
+
c
=
b
+
c


\{\displaystyle a+c=b+c\}

![\{\displaystyle a+c=b+c\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a8d7c402d7bd2bba2f1538877a9f92b458c4f68) для любога *c*

Калі

a

{\displaystyle a=b}

$\{\displaystyle a=b\}$ і

c

{\displaystyle c=d}

$\{\displaystyle c=d\}$ , то

a c

{\displaystyle ac}

$\{\displaystyle ac\}$ =

b d .

{\displaystyle bd.}

$\{\displaystyle bd.\}$ (мультыплікатыўнасць роўнасці) + Калі

a
=
b


\{\displaystyle a=b\}

![\{\displaystyle a=b\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1956b03d1314c7071ac1f45ed7b1e29422dcfcc4), то 



a
c
=
b
c


\{\displaystyle ac=bc\}

![\{\displaystyle ac=bc\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d280528b8755df793b774265a3be5c4569814fa) для любога *c*

Калі значэнні двух сімвалаў супадаюць, то замест аднаго можна падставіць другі (прынцып падстаноўкі).
Калі

{\displaystyle a>b}

$\{\displaystyle a>b\}$ і

{\displaystyle b>c}

$\{\displaystyle b>c\}$ , то

{\displaystyle a>c}

$\{\displaystyle a>c\}$ (транзітыўнасць парадку).

Калі

{\displaystyle a>b}

$\{\displaystyle a>b\}$ , то

a + c

b + c

{\displaystyle a+c>b+c}

$\{\displaystyle a+c>b+c\}$ для любога c.

Калі

{\displaystyle a>b}

$\{\displaystyle a>b\}$ і

{\displaystyle c>0}

$\{\displaystyle c>0\}$ , то

a c

b c .

{\displaystyle ac>bc.}

$\{\displaystyle ac>bc.\}$

Калі

{\displaystyle a>b}

$\{\displaystyle a>b\}$ і

c < 0

{\displaystyle c<0}

$\{\displaystyle c<0\}$ , то

a c < b c .

{\displaystyle ac<bc.}

$\{\displaystyle ac<bc.\}$

Некаторыя алгебраічныя тоеснасці

Гл. таксама: Біном Ньютана і Формулы скарочанага множання

( a + b ) ( a − b )

−

{\displaystyle (a+b)(a-b)=a^{2}-b^{2}}

$\{\displaystyle (a+b)(a-b)=a^\{2\}-b^\{2\}\}$

( a + b

)

2 a b +

;

( a − b

)

− 2 a b +

{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2};\qquad (a-b)^{2}=a^{2}-2ab+b^{2}}

$\{\displaystyle (a+b)^\{2\}=a^\{2\}+2ab+b^\{2\};\qquad (a-b)^\{2\}=a^\{2\}-2ab+b^\{2\}\}$

( a + b

)

b + 3 a

;

( a − b

)

− 3

b + 3 a

−

{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3};\qquad (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}}

$\{\displaystyle (a+b)^\{3\}=a^\{3\}+3a^\{2\}b+3ab^\{2\}+b^\{3\};\qquad (a-b)^\{3\}=a^\{3\}-3a^\{2\}b+3ab^\{2\}-b^\{3\}\}$

= ( a + b ) (

− a b +

) ;

−

= ( a − b ) (

a b +

)

{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2});\qquad a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})}

$\{\displaystyle a^\{3\}+b^\{3\}=(a+b)(a^\{2\}-ab+b^\{2\});\qquad a^\{3\}-b^\{3\}=(a-b)(a^\{2\}+ab+b^\{2\})\}$ Рашэнне ўраўненняў

Асноўны артыкул: Ураўненне Ураўненне — гэта роўнасць віду:

f (

… )

g (

… ) .

{\displaystyle f(x_{1},x_{2}\dots )=g(x_{1},x_{2}\dots ).}

$\{\displaystyle f(x_\{1\},x_\{2\}\dots )=g(x_\{1\},x_\{2\}\dots ).\}$ Рашэнне ўраўнення — задача па знаходжанні такіх значэнняў аргументаў, пры якіх гэта роўнасць дасягаецца. На магчымыя значэнні аргументаў могуць накладвацца дадатковыя ўмовы (цэлалікавасці, рэчаіснасці і т. д.). Рашэнне ўраўненняў — адна з галоўных задач алгебры і наогул матэматыкі, у ходзе гістарычнага развіцця навукі былі распрацаваны шматлікія метады (алгарытмы) для розных разнавіднасцей гэтай задачы.

Гісторыя

Асноўны артыкул: Гісторыя алгебры Ідэя запісваць агульныя ўласцівасці лікаў і вылічальныя алгарытмы на асаблівай сімвалічнай метамове з’явілася даўно, аднак першапачаткова літарнымі сімваламі ва ўраўненнях абазначаліся толькі невядомыя велічыні, значэнні якіх трэба знайсці, а для іншых членаў ураўнення запісваліся канкрэтныя лікавыя значэнні. Думка пра тое, што вядомыя велічыні (каэфіцыенты) таксама карысна для агульнасці абазначаць сімваламі, прабівала сабе шлях павольна.

Упершыню, наколькі можна меркаваць па старажытных сачыненнях, што дайшлі да нас, развітая алгебраічная сістэма паяўляецца ў «Арыфметыцы» Дыяфанта (4 ст.). Верагодна, у яго былі папярэднікі, як яны былі ў Эўкліда, Архімеда і іншых, аднак ні пра людзей, ні пра працы, на якія мог абапірацца гэты выдатны алгебраіст, нічога не вядома. Ды і паслядоўнікаў у яго не было да 15 ст. Зрэшты, у Еўропе з перакладам «Арыфметыкі» пазнаёміліся толькі ў 16 ст., і метады Дыяфанта аказалі велізарны ўплыў на Віета і Ферма.

Асноўная праблематыка «Арыфметыкі» — знаходжанне рацыянальных рашэнняў нявызначаных ураўненняў (мнагачленаў адвольнай ступені) з рацыянальнымі каэфіцыентамі. У Дыяфанта выкарыстоўваецца літарная сімволіка, праўда, па-ранейшаму толькі для невядомых. Ва ўводзінах да «Арыфметыкі» Дыяфант прымае наступныя абазначэнні: невядомую ён называе «лікам» і абазначае літарай ξ, квадрат невядомай — сімвалам

{\displaystyle \delta ^{\nu }}

$\{\displaystyle \delta ^\{\nu \}\}$ і т. д. Асаблівымі сімваламі абазначаліся адмоўныя ступені, знак роўнасці і нават, здаецца, адмоўныя лікі (ёсць нават правіла знакаў: мінус на мінус дае плюс). Усё іншае выражаецца словамі. Сфармуляваны многія звыклыя нам правілы алгебры: змена знака пры пераносе ў іншую частку ўраўнення, скарачэнне агульных членаў і інш.

Індыйскія матэматыкі сярэдневякоўя таксама далёка прасунуліся ў алгебры; іх сімволіка багацейшая, чым у Дыяфанта, хоць некалькі грувасткая (засмечана словамі).

У Еўропе, у кнігах «Арыфметыка» і «Аб дадзеных ліках» Іардана Немарарыя (13 ст.) бачацца зародкі сімвалічнай алгебры, якая яшчэ не аддзялілася ад геаметрыі. У яго, а таксама ў Фібаначы ўжо сустракаюцца выразы, падобныя да «a коней за f дзён з’ядаюць e мер аўса». Аднак у агульную канцэпцыю выкладання сімвалізм у іх яшчэ не ўключаны.

Найбуйнейшы алгебраіст 15 ст. Лука Пачолі ўводзіць свой аналаг алгебраічнай сімволікі, яшчэ не вельмі агульны і не вельмі зручны.

Канцэптуальную рэформу і карэнныя паляпшэнні алгебраічнага мовы ўвёў у канцы 16 ст. Франсуа Віет, адвакат па прафесіі, матэматык па схільнасці душы. Ён выразна ўяўляў сабе канчатковую мэту — распрацоўку «новага злічэння», свайго роду абагульненай арыфметыкі. Віет абазначаў літарамі ўсе каэфіцыенты (дарэчы, іменна Віет прыдумаў гэты тэрмін). Усе задачы рашаюцца ў агульным выглядзе, і толькі потым прыводзяцца лікавыя прыклады. Віет свабодна прымяняе алгебраічныя пераўтварэнні, замену пераменных і іншыя алгебраічныя прыёмы.

Сістэма Віета выклікала ўсеагульнае захапленне. Яна дазволіла апісаць законы арыфметыкі і алгарытмы з неймавернымі раней агульнасцю і кампактнасцю, аблягчыла і паглыбіла даследаванне агульных лікавых законаў. Аднак сімволіка Віета была непадобная на сучасную, месцамі грувасткая, і навукоўцы розных краін прыступілі да яе ўдасканалення.

Англічанін Томас Хэрыят у сваёй пасмяротна выдадзенай (1631) працы ўжо вельмі блізкі да сучаснай сімволікі: ён абазначае зменныя малымі літарамі, а не вялікімі, як у Віета, выкарыстоўвае знак роўнасці, а таксама прыдуманыя ім сімвалы параўнання «>» і «<».

Практычна сучасны выгляд алгебраічнай сімволіцы надаў Рэнэ Дэкарт (сярэдзіна 17 ст., трактат «Геаметрыя»). Вынікам і завяршэннем гэтага працэсу стала «Універсальная арыфметыка» Ньютана. Некаторыя з тых тонкасцей, што засталіся, удакладніў Эйлер.

Гл. таксама

Зноскі

Літаратура

Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6.
Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.

Тэмы гэтай старонкі (4):
Вікіпедыя:Старонкі з модулем Hatnote з чырвонай спасылкай
Элементарная матэматыка
Алгебра
Элементарная алгебра