Лагарыфм
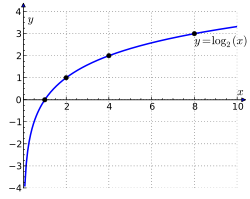
Лагары́фм ліку x па аснове b (ад грэч.: λόγος — «слова», «дачыненне» і ἀριθμός — «лік»[1]) — такое значэнне ступені, у якую трэба ўзвесці лік b, т. зв. асно́ву, каб атрымаць значэнне x. Запіс
log
b
a
{\displaystyle \log _{b}a}
a
{\displaystyle a}
b
{\displaystyle b}
З азначэння вынікае, што знаходжанне
x
log
b
a
{\displaystyle x=\log _{b}a}
b
x
= a .
{\displaystyle b^{x}=a.}
Вылічэнне лагарыфма называецца лагарыфмава́ннем.
Лагарыфмы маюць цікавыя ўласцівасці, якія дазваляюць спрашчаць працаёмкія вылічэнні[2]. Пры пераходзе «ў свет лагарыфмаў» множанне замяняецца на значна прасцейшае складанне, дзяленне — на адыманне, а ўзвядзенне ў ступень і здабыванне кораня ператвараюцца адпаведна ў множанне і дзяленне на паказчык ступені. Лаплас казаў, што вынаходніцтва лагарыфмаў, «скараціўшы працу астранома, падвоіла яго жыццё»[3]. У прыкладаннях аснова b лагарыфма і лагарыфмуемы лік (аргумент лагарыфма) звычайна рэчаісныя. Тым не менш, існуе шэраг праблем (у тым ліку і прыкладных), дзе карысным аказваецца так званы камплексны лагарыфм.
Азначэнне лагарыфмаў і табліцу іх значэнняў (для трыганаметрычных функцый) упершыню надрукаваў у 1614 годзе шатландскі матэматык Джон Непер. Лагарыфмічныя табліцы, пашыраныя і ўдакладненыя іншымі матэматыкамі, паўсюдна выкарыстоўваліся ў навуковых і інжынерных разліках больш за тры стагоддзі, пакуль не з’явіліся электронныя вылічальныя машыны.
З цягам часу высветлілася, што лагарыфмічная функцыя
y
log
b
x
{\displaystyle y=\log _{b}x}
Рэчаісны лагарыфм
Лагарыфм
x
log
b
a
{\displaystyle x=\log _{b}a}
b
x
= a .
{\displaystyle b^{x}=a.}
b
1
{\displaystyle b=1}
a ≠ 1
{\displaystyle a\neq 1}
a
1
{\displaystyle a=1}
b
{\displaystyle b}
b
x
{\displaystyle b^{x}}
a
{\displaystyle a}
|
Як вядома, паказчыкавая функцыя
y
b
x
{\displaystyle y=b^{x}}
b
{\displaystyle b}
Найбольш шырокі ўжытак і шматлікія дастасаванні маюць наступныя віды лагарыфмаў:
ln x
{\displaystyle \ln x}
lg x
{\displaystyle \lg x}
log
2
x
{\displaystyle \log _{2}x}
lb x
{\displaystyle \operatorname {lb} x}
Уласцівасці
Асноўная лагарыфмічная тоеснасць
З азначэння лагарыфма вынікае асноўная лагарыфмічная тоеснасць[6]:
- a
log
a
x
= x
{\displaystyle a^{\log _{a}x}=x}
- log
a
(
a
x
)
= x
{\displaystyle \log _{a}\left(a^{x}\right)=x}
Вывад: з роўнасці двух рэчаісных лагарыфмаў вынікае роўнасць лагарыфмаваных выразаў. Сапраўды, калі
log
a
b
log
a
c
{\displaystyle \log _{a}b=\log _{a}c}
a
log
a
b
=
a
log
a
c
{\displaystyle a^{\log _{a}b}=a^{\log _{a}c}}
b
c .
{\displaystyle b=c.}
Лагарыфмы адзінкі і ліку, роўнага аснове
- log
a
1
0 ,
{\displaystyle \log _{a}1=0,}
- log
a
a
{\displaystyle \log _{a}a=1.}
Арыфметычныя ўласцівасці лагарыфма
- Лагарыфм здабытку:
log
a
( x y )
log
a
( x ) +
log
a
( y )
{\displaystyle \log _{a}(xy)=\log _{a}(x)+\log _{a}(y)}
- Лагарыфм дзелі:
log
a
(
x y
)
=
log
a
( x ) −
log
a
( y )
{\displaystyle \log _{a}\left({\frac {x}{y}}\right)=\log _{a}(x)-\log _{a}(y)}
- Лагарыфм ступені:
log
a
(
x
p
)
p
log
a
( x )
{\displaystyle \log _{a}(x^{p})=p\log _{a}(x)}
- Лагарыфм кораня:
log
a
x
p
=
log
a
( x )
p
{\displaystyle \log _{a}{\sqrt[{p}]{x}}={\frac {\log _{a}(x)}{p}}}
![\{\displaystyle \log _\{a\}\{\sqrt[\{p\}]\{x\}\}=\{\frac \{\log _\{a\}(x)\}\{p\}\}\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ece430566cd091b2e5ceaf74f52fee70f36b9f0f)
- Калі аснова лагарыфма ёсць ступень некаторага выразу:
log
a
k
b
1 k
log
a
b .
{\displaystyle \log _{a^{k}}b={\frac {1}{k}}\log _{a}b.}
a
k
{\displaystyle a^{k}}
a
{\displaystyle a}
Вынікі:
- log
a
n
b
n
log
a
b ;
{\displaystyle \log _{\sqrt[{n}]{a}}b=n\log _{a}b;}
![\{\displaystyle \log _\{\sqrt[\{n\}]\{a\}\}b=n\log _\{a\}b;\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22819d06c9c8bff827fa4f91f0b7a30f517d8c7d)
log
a
k
b
p
=
p k
log
a
b
;
{\displaystyle \log _{a^{k}}{b^{p}}={\frac {p}{k}}\log _{a}{b};}
log
a
k
b
k
=
log
a
b .
{\displaystyle \log _{a^{k}}b^{k}=\log _{a}b.}
- Яшчэ адна карысная тоеснасць:
c
log
a
b
=
b
log
a
c
{\displaystyle c^{\log _{a}b}=b^{\log _{a}c}}
a
{\displaystyle a}
Існуе відавочнае абагульненне прыведзеных формул:
log
a
|
x y
|
=
log
a
|
x
|
log
a
|
y
|
{\displaystyle \log _{a}|xy|=\log _{a}|x|+\log _{a}|y|}
log
a
|
x y
|
=
log
a
|
x
|
−
log
a
|
y
|
{\displaystyle \log _{a}\left|{\frac {x}{y}}\right|=\log _{a}|x|-\log _{a}|y|}
log
a
(
x
1
x
2
…
x
n
)
log
a
(
x
1
) +
log
a
(
x
2
) + ⋯ +
log
a
(
x
n
)
{\displaystyle \log _{a}(x_{1}x_{2}\dots x_{n})=\log _{a}(x_{1})+\log _{a}(x_{2})+\dots +\log _{a}(x_{n})}
x , y
{\displaystyle x,y}
- Знайсці ў табліцах лагарыфмы лікаў
x , y
{\displaystyle x,y}
x ⋅ y
{\displaystyle x\cdot y}
Дзяленне, якое без дапамогі лагарыфмаў істотна больш працаёмкае чым множанне, выконвалася па таму ж алгарытму, толькі з заменай складання лагарыфмаў на адыманне. Гэтак жа спрашчаліся ўзвядзенне ў ступень і здабыванне кораня.
Замена асновы лагарыфма
- Ад лагарыфма
log
a
b
{\displaystyle \log _{a}b}
a
{\displaystyle a}
c
{\displaystyle c}
log
a
b
log
c
b
log
c
a
{\displaystyle \log _{a}b={\frac {\log _{c}b}{\log _{c}a}}}
- Вынік: перастаноўка асновы і лагарыфмуемага выразу:
log
a
b
1
log
b
a
{\displaystyle \log _{a}b={\frac {1}{\log _{b}a}}}
Лагарыфмічная функцыя
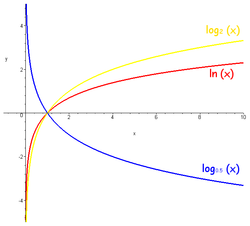
Асноўныя уласцівасці
Калі разглядаць лагарыфмаваны лік як зменную, мы атрымаем лагарыфмічную функцыю
y
log
a
x
{\displaystyle y=\log _{a}x}
a
0 ; a ≠ 1 ; x
0
{\displaystyle a>0;\ a\neq 1;x>0}
- Абсяг вызначэння:
x
0
{\displaystyle x>0}
- Абсяг значэнняў:
E ( y )
( − ∞ ; + ∞ )
{\displaystyle E(y)=(-\infty ;+\infty )}
Гэта крывая часта называецца лагарыфмікай[7].
- З формулы замены асновы лагарыфма відаць, што графікі лагарыфмічных функцый з рознымі асновамі, большымі за адзінку, адрозніваюцца адзін ад аднаго толькі расцяжэннем уздоўж восі
y
{\displaystyle y}
log
b
x
log
a
x
log
a
b
{\displaystyle \log _{b}x={\frac {\log _{a}x}{\log _{a}b}}}
- Графікі для асноў
a
{\displaystyle a}
1
/
a
{\displaystyle 1/a}
- З азначэння вынікае, што лагарыфмічная функцыя
y
log
a
x
{\displaystyle y=\log _{a}x}
y
a
x
{\displaystyle y=a^{x}}
- Лагарыфмічная функцыя строга нарастае пры
a
1
{\displaystyle a>1}
0 < a < 1
{\displaystyle 0<a<1}
( 1 ; 0 )
{\displaystyle (1;0)}
- Вось ардынат
( x
0 )
{\displaystyle (x=0)}
lim
x → + 0
log
a
x
− ∞
{\displaystyle \lim _{x\to +0}\log _{a}x=-\infty }
a
1 ;
{\displaystyle a>1;}
lim
x → + 0
log
a
x
∞
{\displaystyle \lim _{x\to +0}\log _{a}x=+\infty }
0 < a < 1.
{\displaystyle 0<a<1.}
- Вытворная лагарыфмічнай функцыі:
(
log
a
x
) ′
=
1
x ln a
{\displaystyle (\log _{a}x)’={\frac {1}{x\ln a}}}
- Першаісная лагарыфмічнай функцыі:
∫
log
a
x
d x
x
log
a
x −
x
ln a
C ,
{\displaystyle \int \log _{a}x,dx=x\log _{a}x-{\frac {x}{\ln a}}+C,}
- З пункту гледжання алгебры, лагарыфмічная функцыя ажыццяўляе (адзіны магчымы) ізамарфізм групы адносна множання дадатных рэчаісных лікаў і групы адносна складання ўсіх рэчаісных лікаў. Іншымі словамі, лагарыфмічная функцыя з’яўляецца адзіным (вызначаным для ўсіх дадатных значэнняў аргумента) непарыўным рашэннем функцыянальнага ўраўнення[8]:
f ( x y )
f ( x ) + f ( y ) .
{\displaystyle f(xy)=f(x)+f(y).}
Натуральны лагарыфм
Асноўны артыкул: Натуральны лагарыфм Прыведзеная вышэй агульная формула вытворнай выглядае найпрасцей у выпадку натуральнага лагарыфма:
d
d x
ln x
1 x
.
{\displaystyle {\frac {d}{dx}}\ln x={\frac {1}{x}}.}
Праінтэграваўшы формулу для вытворнай у прамежку ад
x
1
{\displaystyle x=1}
x
b
{\displaystyle x=b}
ln b
∫
1
b
d x
x
.
{\displaystyle \ln b=\int \limits _{1}^{b}{\frac {dx}{x}}.}
y
1 x
{\displaystyle y={\frac {1}{x}}}
Нявызначаны інтэграл ад натуральнага лагарыфма лёгка знайсці інтэграваннем па частках:
∫
ln x
d
x
= x ln x − x + C .
{\displaystyle \int {\ln x,\mathrm {d} x}=x\ln x-x+C.}
f ( x )
{\displaystyle f(x)}
d
d x
ln ( f ( x ) )
f ′
( x )
f ( x )
.
{\displaystyle {\frac {d}{dx}}\ln(f(x))={\frac {f’(x)}{f(x)}}.}
Раскладанне ў рад і вылічэнне натуральнага лагарыфма
Раскладзём натуральны лагарыфм у рад Тэйлара каля адзінкі:
ln ( 1 + x )
x −
x
2
2
x
3
3
−
x
4
4
… .
{\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots .}
− 1 < x ≤ 1.
{\displaystyle -1<x\leq 1.}
ln 2
1 −
1 2
1 3
−
1 4
… .
{\displaystyle \ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots .}
ln
(
1 + x
1 − x
)
= 2
(
x +
x
3
3
x
5
5
x
7
7
…
)
.
{\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right).}
Карыстацца апошняй формулай трэба так. Няхай
Z
{\displaystyle Z}
- З ураўнення
Z
1 + x
1 − x
{\displaystyle Z={\frac {1+x}{1-x}}}
x
{\displaystyle x}
x
Z − 1
Z + 1
.
{\displaystyle x={\frac {Z-1}{Z+1}}.}
x
{\displaystyle x}
ln Z
{\displaystyle \ln Z}
Дадзены алгарытм ужо прыдатны да выкарыстання на практыцы пры вылічэнні значэнняў лагарыфмаў, аднак ён не найлепшы з пункту гледжання працаёмкасці. Існуюць больш дзейсныя алгарытмы[9].
Гранічныя суадносіны
Прывядзём некалькі карысных граніц, якія ўтрымліваюць лагарыфмы[10].
lim
x → 0
log
a
( 1 + x )
x
=
log
a
e
1
ln a
{\displaystyle \lim _{x\to 0}{\frac {\log _{a}(1+x)}{x}}=\log _{a}e={\frac {1}{\ln a}}}
lim
x → + 0
x
b
log
a
x
0
( b
0 )
{\displaystyle \lim _{x\to +0}x^{b}\log _{a}x=0\quad (b>0)}
lim
x → + ∞
log
a
x
x
b
= 0
( b
0 )
{\displaystyle \lim _{x\to +\infty }{\frac {\log _{a}x}{x^{b}}}=0\quad (b>0)}
ln x
lim
n → ∞
n
(
x
n
− 1
)
=
lim
n → ∞
n
(
1 −
1
x
n
)
{\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}
![\{\displaystyle \ln x=\lim _\{n\to \infty \}n\left(\{\sqrt[\{n\}]\{x\}\}-1\right)=\lim _\{n\to \infty \}n\left(1-\{\frac \{1\}\{\sqrt[\{n\}]\{x\}\}\}\right)\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7901ca277e9fe1a5be535f262d7d4a84fc51a3f)
ln x
lim
h → 0
x
h
− 1
h
{\displaystyle \ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}}
Іншыя ўласцівасці
- З тэарэмы Гельфонда вынікае, што калі
a , b
{\displaystyle a,b}
a ≠ 1
{\displaystyle a\neq 1}
log
a
b
{\displaystyle \log _{a}b}
p q
{\displaystyle {\frac {p}{q}}}
a , b
{\displaystyle a,b}
a
p
=
b
q
{\displaystyle a^{p}=b^{q}}
- Сума
∑
k
1
n
1 k
{\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}}
n
{\displaystyle n}
ln n + C
{\displaystyle \ln n+C}
C ≈ 0,577 215664 …
{\displaystyle C\approx 0{,}577215664\dots }
— Камплексны лагарыфм
Асноўны артыкул: Камплексны лагарыфм Вызначэнне і ўласцівасці
Для камплексных лікаў лагарыфм вызначаецца гэтак жа, як рэчаісны. На практыцы выкарыстоўваецца амаль выключна натуральны камплексны лагарыфм, які пазначаецца
L n
z
{\displaystyle \mathrm {Ln} ,z}
w
{\displaystyle w}
e
w
= z
{\displaystyle e^{w}=z}
У полі камплексных лікаў рашэнне гэтага ўраўнення, у адрозненне ад рэчаіснага выпадку, не вызначана адназначна. Напрыклад, згодна з тоеснасцю Эйлера,
e
π i
= − 1
{\displaystyle ~e^{\pi i}=-1}
e
− π i
=
e
3 π i
=
e
5 π i
⋯
− 1
{\displaystyle ~e^{-\pi i}=e^{3\pi i}=e^{5\pi i}\dots =-1}
2 π
{\displaystyle ~2\pi }
w
L n
z
{\displaystyle ~w=\mathrm {Ln} ,z}
Камплексны нуль не мае лагарыфма, паколькі камплексная экспанента не прыймае нулявога значэння. Ненулявое
z
{\displaystyle z}
z
r ⋅
e
i φ
{\displaystyle z=r\cdot e^{i\varphi }}
L n
z
{\displaystyle \mathrm {Ln} ,z}
L n
z
ln r + i
(
φ + 2 π k
)
{\displaystyle \mathrm {Ln} ,z=\ln r+i\left(\varphi +2\pi k\right)}
ln
r
ln
|
z
|
{\displaystyle \ln ,r=\ln ,|z|}
k
{\displaystyle k}
|
Камплексны лагарыфм існуе для любога , і яго рэчаісная частка вызначаецца адназначна, у той час як уяўная частка мае бясконцае мноства значэнняў, якія адрозніваюцца на цэлае кратнае . |
З формулы відаць, што ў аднаго і толькі аднаго са значэнняў уяўная частка знаходзіцца ў інтэрвале
( − π , π ]
{\displaystyle ~(-\pi ,\pi ]}
![{\displaystyle ~(-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bf5bcf13ea590731487de197bae7d32a72526ca). Гэта значэнне называецца галоўным значэннем комплекснага натуральнага лагарыфма. Адпаведная (ужо адназначная) функцыя называецца галоўнай галіной лагарыфма і пазначаецца
ln
z
{\displaystyle \ln ,z}
ln
z
{\displaystyle \ln ,z}
z
{\displaystyle z}
З прыведзенай формулы таксама вынікае, што рэчаісная частка лагарыфма вызначаецца наступным чынам праз кампаненты аргумента:
Re ( ln ( x + i y ) )
1 2
ln (
x
2
y
2
)
{\displaystyle \operatorname {Re} (\ln(x+iy))={\frac {1}{2}}\ln(x^{2}+y^{2})}
− ∞ .
{\displaystyle -\infty .}
Прыклады значэнняў комплекснага лагарыфма
Прывядзем галоўнае значэнне лагарыфма (
ln
{\displaystyle \ln }
L n
{\displaystyle \mathrm {Ln} }
ln ( 1 )
0 ;
L n
( 1 )
2 k π i
{\displaystyle \ln(1)=0;;\mathrm {Ln} (1)=2k\pi i}
ln ( − 1 )
i π ;
L n
( − 1 )
( 2 k + 1 ) i π
{\displaystyle \ln(-1)=i\pi ;;\mathrm {Ln} (-1)=(2k+1)i\pi }
ln ( i )
i
π 2
;
L n
( i )
i
4 k + 1
2
π
{\displaystyle \ln(i)=i{\frac {\pi }{2}};;\mathrm {Ln} (i)=i{\frac {4k+1}{2}}\pi }
i π
ln ( − 1 )
ln ( ( − i
)
2
)
2 ln ( − i )
2 ( − i π
/
2 )
− i π
{\displaystyle i\pi =\ln(-1)=\ln((-i)^{2})=2\ln(-i)=2(-i\pi /2)=-i\pi }
k
− 1
{\displaystyle k=-1}
log
a
(
b
p
)
= p
log
a
b
{\displaystyle \log _{a}{(b^{p})}=p~\log _{a}b}
Камплексная лагарыфмічная функцыя і рыманавая паверхня
У камплексным аналізе замест разгляду мнагазначных функцый на камплекснай плоскасці прынята іншае рашэнне: разглядаць функцыю як адназначную, але вызначаную не на плоскасці, а на больш складанай разнастайнасці, якоая называецца рыманавай паверхняй[13]. Камплексная лагарыфмічная функцыя таксама адносіцца да гэтай катэгорыі: яе вобраз складаецца з бясконцага ліку галін, закручаных ў выглядзе спіралі. Гэтая паверхню бесперапынная і аднасувязная. Адзіны нуль у функцыі (першага парадку) атрымліваецца пры
z
1
{\displaystyle z=1}
z
0
{\displaystyle z=0}
z
∞
{\displaystyle z=\infty }
У сілу аднасувязнасці рыманавая паверхня лагарыфма з’яўляецца універсальнай накрываючай[14] для камплекснай плоскасці без пункту
0
{\displaystyle 0}
Аналітычны працяг
Лагарыфм камплекснага ліку таксама можа быць вызначаны як аналітычны працяг рэчаіснага лагарыфма на ўсю камплексную плоскасць. Хай крывая
Γ
{\displaystyle \Gamma }
w
{\displaystyle w}
Γ
{\displaystyle \Gamma }
ln z
∫
Γ
d u
u
{\displaystyle \ln z=\int \limits _{\Gamma }{du \over u}}
Γ
{\displaystyle \Gamma }
ln ( w z )
ln w + ln z , ∀ z , w ∈ Γ : z w ∈ Γ
{\displaystyle \ln(wz)=\ln w+\ln z,~\forall z,w\in \Gamma \colon zw\in \Gamma }
2 π
{\displaystyle 2\pi }
( − π , π ]
{\displaystyle ~(-\pi ,\pi ]}
![{\displaystyle ~(-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bf5bcf13ea590731487de197bae7d32a72526ca). Калі разгледзець усе галіны функцыі, то бесперапыннасць мае месца ва ўсіх пунктах, акрамя нуля, дзе функцыя не вызначана. Калі дазволіць крывой
Γ
{\displaystyle \Gamma }
З формулы аналітычнага працягу вынікае, што на любой галіне лагарыфма:
d
d z
ln z
1 z
{\displaystyle {\frac {d}{dz}}\ln z={1 \over z}}
Для любой акружнасці
S
{\displaystyle S}
0
{\displaystyle 0}
∮
S
d z
z
= 2 π i
{\displaystyle \oint \limits _{S}{dz \over z}=2\pi i}
Можна таксама вызначыць аналітычнае працяг комплекснага лагарыфма з дапамогай вышэйпрыведзеных радоў: раду 1 або раду 2, — абагульненых на выпадак камплекснага аргументу. Аднак з выгляду гэтых радоў вынікае, што ў адзінцы сума раду роўная нулю, шэта значыць рад адносіцца толькі да галоўнай галіны шматзначнай функцыі камплекснага лагарыфма. Радыус збежнасці абодвух радоў роўны 1.
Сувязь са зваротнымі трыганаметрычнымі і гіпербалічнымі функцыямі
Паколькі камплексныя трыганаметрычныя функцыі звязаныя з экспанентай (формула Эйлера), то камплексны лагарыфм як зваротная да экспаненты функцыя звязаны са зваротнымі трыганаметрычнымі функцыямі[16]:
Arcsin z
− i Ln ( i z +
1 −
z
2
)
{\displaystyle \operatorname {Arcsin} z=-i\operatorname {Ln} (iz+{\sqrt {1-z^{2}}})}
Arccos z
− i Ln ( z + i
1 −
z
2
)
{\displaystyle \operatorname {Arccos} z=-i\operatorname {Ln} (z+i{\sqrt {1-z^{2}}})}
Arctg z
−
i 2
ln
1 + z i
1 − z i
k π
( z ≠ ± i )
{\displaystyle \operatorname {Arctg} z=-{\frac {i}{2}}\ln {\frac {1+zi}{1-zi}}+k\pi ;(z\neq \pm i)}
Arcctg z
−
i 2
ln
z i − 1
z i + 1
k π
( z ≠ ± i )
{\displaystyle \operatorname {Arcctg} z=-{\frac {i}{2}}\ln {\frac {zi-1}{zi+1}}+k\pi ;(z\neq \pm i)}
Arsh z
Ln ( z +
z
2
1
)
{\displaystyle \operatorname {Arsh} z=\operatorname {Ln} (z+{\sqrt {z^{2}+1}})}
Arch z
Ln
(
z +
z
2
− 1
)
{\displaystyle \operatorname {Arch} z=\operatorname {Ln} \left(z+{\sqrt {z^{2}-1}}\right)}
Arth z
1 2
Ln
(
1 + z
1 − z
)
{\displaystyle \operatorname {Arth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {1+z}{1-z}}\right)}
Arcth z
1 2
Ln
(
z + 1
z − 1
)
{\displaystyle \operatorname {Arcth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {z+1}{z-1}}\right)}
— зваротны гіпербалічны катангенс
Ужыванне на практыцы
Табліцы лагарыфмаў
З уласцівасцей лагарыфма вынікае, што замест працаёмкага множання шматзначных лікаў дастаткова адшукаць (па табліцах) і скласці іхнія лагарыфмы, а потым па тых жа табліцах («Антылагарыфмы») выканаць ступеняванне, г.зн. знайсці значэнне па яго лагарыфму. Выкананне дзялення адрозніваецца толькі тым, што лагарыфмы адымаюцца.
Першыя табліцы лагарыфмаў выдаў Джон Непер (1614), і яны ўтрымівалі толькі лагарыфмы трыганаметрычных функцый, прычым з памылкамі. Незалежна ад яго свае табліцы надрукаваў Ёст Бюргі, друг Кеплера (1620). У 1617 годзе оксфардскі прафесар матэматыкі Генры Брыгс выдаў табліцы, якія ўжо ўключалі дзесятковыя лагарыфмы лікаў ад 1 да 1000, з 8 (пазней — з 14) знакамі. Але і ў табліцах Брыгса выявіліся памылкі. Першае безпамылковае выданне на аснове табліц Георга Вегі (1783) з’явілася толькі ў 1857 годзе ў Берліне (табліцы Брэмікера, Carl Bremiker)[18].
У Расіі першыя табліцы лагарыфмаў былі выдадзены ў 1703 годзе пры ўдзеле Л. П. Магніцкага[19]. У СССР было выдадзена некалькі зборнікаў табліц лагарыфмаў[20]:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Табліцы Брадзіса, выдаваныя з 1921 года, выкарыстоўваліся ў навучальных установах і ў інжынерных разліках, якія не патрабавалі вялікай дакладнасці. Яны ўтрымлівалі мантысы дзесятковых лагарыфмаў і трыганаметрычных функцый, натуральныя лагарыфмы і некаторыя іншыя карысныя разліковыя прылады.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Адмысловы зборнік для дакладных вылічэнняў.
- Бремикер К. Логарифмо-тригонометрические таблицы. М.: Наука, 1962. 664 с. Класічныя шасцізначныя табліцы, зручныя для разлікаў з трыганаметрычнымі функцыямі.
- Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6-е издание, М.: Наука, 1972.
- Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
- Десятизначные таблицы логарифмов комплексных чисел. М., 1952.
Лагарыфмічная лінейка
Асноўны артыкул: Лагарыфмічная лінейка У 1620-я гады Эдмунд Уінгейт і Уільям Оўтрэд вынайшлі першую лагарыфмічную лінейку, якая да з’яўлення кішэнных калькулятараў была незаменнай вылічальнай прыладай інжынера[21]. З дапамогай гэтай невялічкай прылады можна было хутка выконваць усе алгебраічныя аперацыі, у тым ліку з трыганаметрычнымі функцыямі[22]. Дакладнасць разлікаў — каля 3 значных лічб.
Гл. таксама
- Камплексны лік
- Паказнікавая функцыя
- Камплексны лагарыфм
- Ступеняванне
- Лагарыфмічная лінейка
- Сістэмы злічэння
- Спіс інтэгралаў ад лагарыфмічных функцый
Крыніцы
Зноскі
- ↑
Краткий словарь иностранных слов. М.: Русский язык, 1984. - ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 184-186.
- ↑
Швецов К. И., Бевз Г. П. Справочник по элементарной математике. Арифметика, алгебра. Киев: Наукова Думка, 1966. § 40. Исторические сведения о логарифмах и логарифмической линейке. - 1 2 Корн Г., Корн Т. Справочник по математике, 1973, с. 34.
- ↑
Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 229. - ↑
Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233. - ↑
Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. - ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 159-160.
- ↑
Sasaki T., Kanada Y. Practically fast multiple-precision evaluation of log(x)(англ.) // Journal of Information Processing. — 1982. — В. 4. — Т. 5. — С. 247–250. - ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 164.
- ↑
Alan Baker. Transcendental number theory. — Cambridge University Press, 1975. — С. 10. — ISBN 978-0-521-20461-3. - ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 520-522.
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 92-94.
- ↑ Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 45-46, 99-100.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 522-526.
- ↑ Корн Г., Корн Т. Справочник по математике, 1973, с. 624.
- ↑ История математики, том II, 1970, с. 62.
- ↑
Гнеденко Б. В. Очерки по истории математики в России, издание 2-е. — М.: КомКнига, 2005. — С. 66. — 296 с. — ISBN 5-484-00123-4. - ↑
Логарифмические таблицы //Большая советская энциклопедия. - ↑ История математики, том II, 1970, с. 65-66.
- ↑
Березин С. И. Счётная логарифмическая линейка. — М.: Машиностроение, 1968.
Спасылкі
На Вікісховішчы ёсць медыяфайлы па тэме Лагарыфм- Colin Byfleet, Educational video on logarithms.
- Edward Wright, Translation of Napier’s work on logarithms Архівавана 27 чэрвеня 2007..
Вікіпедыя:Істотныя артыкулы
Элементарныя функцыі
Лагарыфмы
Вікіпедыя:Старонкі з модулем Hatnote з чырвонай спасылкай