wd wp Пошук: ⬜

Трохвугольнік

Тро́хвуго́льнік — геаметрычная фігура, утвораная трыма адрэзкамі, якія злучаюць тры пункты, што не ляжаць на адной прамой. Гэтыя адрэзкі называюцца старанамі (бакамі) трохвугольніка, а пункты, злучаныя старанамі, — яго вяршынямі.

Трохвугольнік — найпрасцейшы з многавугольнікаў.

Вяршыні трохвугольніка звычайна абазначаюцца вялікімі лацінскімі літарамі (A, B, C), велічыні вуглоў пры адпаведных вяршынях — грэчаскімі літарамі (α, β, γ), а даўжыні процілеглых старон — маленькімі лацінскімі літарамі (a, b, c).

Трохвугольнік з’яўляецца шматграннікам. У еўклідавай геаметрыі трохвугольнік адназначна задае плоскасць. Усе трохвугольнікі з’яўляюцца плоскімі фігурамі.

Класіфікацыя трохвугольнікаў


Віды трохвугольнікаў паводле велічыні вуглоў
Востравугольны	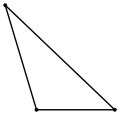Тупавугольны	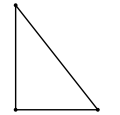Прамавугольны

Паводле велічыні вуглоў

Раз сума вуглоў трохвугольніка роўная 180°, то не менш чым два вуглы ў трохвугольніку павінны быць вострымі (меншымі за 90°). Вылучаюць наступныя віды трохвугольнікаў:

Калі ўсе вуглы трохвугольніка вострыя, то трохвугольнік завецца востравугольным;
Калі адзін з вуглоў трохвугольніка тупы (большы за 90°), то трохвугольнік завецца тупавугольным;
Калі адзін з вуглоў трохвугольніка прамы (роўны 90°), то трохвугольнік завецца прамавугольным. Дзве стараны, якія ўтвараюць прамы вугал, завуцца катэтамі, а старана, процілеглая прамому вуглу, завецца гіпатэнузай.


Віды трохвугольнікаў паводле колькасці роўных старон
Рознастаронні	Раўнабедраны	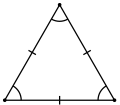Роўнастаронні

Паводле колькасці роўных старон

Рознастароннім называецца трохвугольнік, у якога даўжыні старон папарна розныя.
Раўнабедраным завецца трохвугольнік, у якога дзве стараны роўныя. Гэтыя стораны завуцца бакавымі, трэцяя старана завецца асновай. У раўнабедраным трохвугольніку вуглы пры аснове роўныя. Вышыня, медыяна і бісектрыса раўнабедранага трохвугольніка, апушчаныя на аснову, супадаюць.
Роўнастароннім завецца трохвугольнік, у якога ўсе тры стараны роўныя. У роўнастароннім трохвугольніку ўсе вуглы роўныя 60°, а цэнтры упісанай і апісанай акружнасцей супадаюць.

Няроўнасць трохвугольніка

Стораны трохвугольніка нельга задаваць адвольна, яны звязаныя наступнымі няроўнасцямі

a < b

{\displaystyle a<b+c}

$\{\displaystyle a<b+c\}$

b < c

{\displaystyle b<c+a}

$\{\displaystyle b<c+a\}$

c < a

{\displaystyle c<a+b}

$\{\displaystyle c<a+b\}$

Калі хаця б у адной з гэтых суадносін мае месца роўнасць, трохвугольнік называецца выраджаным. Далей усюды маецца на ўвазе нявыраджаны выпадак.

Прыкметы роўнасці трохвугольнікаў

Трохвугольнік адназначна можна вызначыць па наступных тройках асноўных элементаў:

a, b, c (роўнасць па трох старанах);
a, b, γ (роўнасць па дзвюх старанах і вуглу паміж імі);
a, β, γ (роўнасць па старане і двух прылеглых вуглах).

Адрэзкі і акружнасці, звязаныя з трохвугольнікам

Акружнасць, датычная ўсіх трох старон трохвугольніка, завецца яго упісанай акружнасцю. Яна вызначана адназначна. Акружнасць, якая праходзіць праз усе тры вяршыні трохвугольніка, завецца яго апісанай акружнасцю. Апісаная акружнасць таксама вызначана адназначна.

Медыянай трохвугольніка, праведзенай з дадзенай вяршыні, завецца адрэзак, які злучае гэту вяршыню з сярэдзінай процілеглай стараны. Усе тры медыяны трохвугольніка перасякаюцца ў адным пункце. Гэты пункт перасячэння называецца цэнтроідам або цэнтрам цяжару трохвугольніка. Апошняя назва звязана з тым, што ў трохвугольніка, зробленага з аднароднага матэрыялу, цэнтр цяжару знаходзіцца ў пункце перасячэння медыян. Цэнтроід дзеліць кожную медыяну ў адносіне 1:2, калі лічыць ад асновы медыяны.

Перпендыкуляр, апушчаны з вяршыні трохвугольніка на процілеглую старану або яе працяг, завецца вышынёй трохвугольніка. Тры вышыні трохвугольніка перасякаюцца ў адным пункце, які называецца ортацэнтрам трохвугольніка.

Бісектрысай трохвугольніка, праведзенай з дадзенай вяршыні, завуць адрэзак, які злучае гэту вяршыню з пунктам на процілеглай старане і дзеліць вугал пры дадзенай вяршыні папалам. Бісектрысы трохвугольніка перасякаюцца ў адным пункце, і гэты пункт супадае з цэнтрам упісанай акружнасці.

У раўнабедраным трохвугольніку бісектрыса, медыяна і вышыня, праведзеныя да асновы, супадаюць. Справядліва і адваротнае: калі бісектрыса, медыяна і вышыня, праведзеныя з адной вяршыні, супадаюць, то трохвугольнік раўнабедраны. Калі трохвугольнік рознастаронні, то для любой яго вяршыні бісектрыса, праведзеная з яе, ляжыць паміж медыянай і вышынёй, праведзенымі з той жа вяршыні.

Сярэдзінныя перпендыкуляры да старон трохвугольніка таксама перасякаюцца ў адным пункце, які супадае з цэнтрам апісанай акружнасці.

Пазаўпісанай акружнасцю завецца акружнасць, датычная аднае стараны трохвугольніка і працягу дзвюх іншых старон.

Сярэдзіны трох старон трохвугольніка, асновы трох яго вышынь і сярэдзіны трох адрэзкаў, якія злучаюць яго вяршыні з артацэнтрам, ляжаць на адной акружнасці, якая называецца акружнасцю дзевяці пунктаў.

У любым трохвугольніку цэнтр цяжару, артацэнтр, цэнтр апісанай акружнасці і цэнтр акружнасці дзевяці пунктаў ляжаць на адной прамой, якая называецца прамою Эйлера.

Суадносіны ў трохвугольніку

Калі вядомыя тры велічыні з шасці (тры стараны і тры вуглы), то астатнія можна знайсці па наступных формулах:

Тэарэма сінусаў

Асноўны артыкул: Тэарэма сінусаў Справядлівыя наступныя суадносіны паміж даўжынямі старон і сінусамі адпаведных процілеглых вуглоў:

sin ⁡ α

sin ⁡ β

sin ⁡ γ

= 2 R ,

{\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R,}

$\{\displaystyle \{\frac \{a\}\{\sin \alpha \}\}=\{\frac \{b\}\{\sin \beta \}\}=\{\frac \{c\}\{\sin \gamma \}\}=2R,\}$ дзе R — радыус апісанай акружнасці.

Гэтыя суадносіны называюцца тэарэмаю сінусаў. Сярод іншага, з тэарэмы вынікае, што калі a < b < c, то α < β < γ.

Тэарэма косінусаў

Асноўны артыкул: Тэарэма косінусаў Ведаючы дзве стараны трохвугольніка і вугал паміж імі, можна вылічыць трэцюю старану па формуле:

c2 = a2 + b2 — 2ab cos γ. Гэта формула называецца тэарэмаю косінусаў і з’яўляецца абагульненнем тэарэмы Піфагора.

Тэарэма пра суму вуглоў трохвугольніка

Асноўны артыкул: Тэарэма аб суме вуглоў трохвугольніка Сума вуглоў любога трохвугольніка раўняецца 180° (π радыян):

α + β + γ = 180° (π) Гэта сцвярджэнне раўназначнае аксіёме паралельнасці Еўкліда.

Іншыя суадносіны

Метрычныя суадносіны ў трохвугольніку, прыведзеныя для трохвугольніка

△ A B C :

{\displaystyle \triangle ABC:}

$\{\displaystyle \triangle ABC:\}$

a b

{\displaystyle {a \over b}={a_{L} \over b_{L}}}

$\{\displaystyle \{a \over b\}=\{a_\{L\} \over b_\{L\}\}\}$

a b ( a + b + c ) ( a + b − c )

a + b

a b −

2 a b cos ⁡

γ 2

a + b

{\displaystyle l_{c}={{\sqrt {ab(a+b+c)(a+b-c)}} \over {a+b}}={\sqrt {ab-a_{L}b_{L}}}={\frac {2ab\cos {\frac {\gamma }{2}}}{a+b}}}

$\{\displaystyle l_\{c\}=\{\{\sqrt \{ab(a+b+c)(a+b-c)\}\} \over \{a+b\}\}=\{\sqrt \{ab-a_\{L\}b_\{L\}\}\}=\{\frac \{2ab\cos \{\frac \{\gamma \}\{2\}\}\}\{a+b\}\}\}$

1 2

2 (

) −

{\displaystyle m_{c}={1 \over 2}{\sqrt {2(a^{2}+b^{2})-c^{2}}}}

$\{\displaystyle m_\{c\}=\{1 \over 2\}\{\sqrt \{2(a^\{2\}+b^\{2\})-c^\{2\}\}\}\}$

= b sin ⁡ α

a sin ⁡ β

2 S

{\displaystyle h_{c}=b\sin \alpha =a\sin \beta ={\frac {2S}{c}}}

$\{\displaystyle h_\{c\}=b\sin \alpha =a\sin \beta =\{\frac \{2S\}\{c\}\}\}$

− 2 R r

{\displaystyle \ d^{2}=R^{2}-2Rr}

$\{\displaystyle \ d^\{2\}=R^\{2\}-2Rr\}$ — формула Эйлера

r R

= 4 sin ⁡

α 2

sin ⁡

β 2

sin ⁡

γ 2

= cos ⁡ α + cos ⁡ β + cos ⁡ γ − 1

{\displaystyle {\frac {r}{R}}=4\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}=\cos \alpha +\cos \beta +\cos \gamma -1}

$\{\displaystyle \{\frac \{r\}\{R\}\}=4\sin \{\frac \{\alpha \}\{2\}\}\sin \{\frac \{\beta \}\{2\}\}\sin \{\frac \{\gamma \}\{2\}\}=\cos \alpha +\cos \beta +\cos \gamma -1\}$ Дзе:

{\displaystyle \ l_{a},l_{b},l_{c}}

$\{\displaystyle \ l_\{a\},l_\{b\},l_\{c\}\}$ — адпаведна бісектрысы вуглоў

{\displaystyle A}

$\{\displaystyle A\}$ ,

{\displaystyle B}

$\{\displaystyle B\}$ і

{\displaystyle C}

$\{\displaystyle C\}$ ,

{\displaystyle \ a_{L},b_{L}}

$\{\displaystyle \ a_\{L\},b_\{L\}\}$ — адрэзкі, на якія бісектрысы

{\displaystyle \ l_{c}}

$\{\displaystyle \ l_\{c\}\}$ дзеліць старану

{\displaystyle \ c}

$\{\displaystyle \ c\}$ ,

{\displaystyle \ m_{a},m_{b},m_{c}}

$\{\displaystyle \ m_\{a\},m_\{b\},m_\{c\}\}$ — медыяны, праведзеныя адпаведна да старон

{\displaystyle a}

$\{\displaystyle a\}$ ,

{\displaystyle b}

$\{\displaystyle b\}$ і

{\displaystyle c}

$\{\displaystyle c\}$ ,

{\displaystyle \ h_{a},h_{b},h_{c}}

$\{\displaystyle \ h_\{a\},h_\{b\},h_\{c\}\}$ — вышыні, апушчаныя адпаведна на стораны

{\displaystyle a}

$\{\displaystyle a\}$ ,

{\displaystyle b}

$\{\displaystyle b\}$ і

{\displaystyle c}

$\{\displaystyle c\}$ ,

{\displaystyle \ r}

$\{\displaystyle \ r\}$ — радыус упісанай акружнасці,

{\displaystyle \ R}

$\{\displaystyle \ R\}$ — радыус апісанай акружнасці,

p

a + b + c

{\displaystyle p={\frac {a+b+c}{2}}}

$\{\displaystyle p=\{\frac \{a+b+c\}\{2\}\}\}$ — паўперыметр,

{\displaystyle \ S}

$\{\displaystyle \ S\}$ — плошча,

{\displaystyle \ d}

$\{\displaystyle \ d\}$ — адлегласць паміж цэнтрамі ўпісанай і апісанай акружнасцей. Плошча трохвугольніка

Найвядомейшая і найпрасцейшая формула:

S

1 2

{\displaystyle S={\frac {1}{2}}bh_{b}}

$\{\displaystyle S=\{\frac \{1\}\{2\}\}bh_\{b\}\}$ Дзе:

{\displaystyle \ b}

$\{\displaystyle \ b\}$ — даўжыня асновы трохвугольніка (старана, да якой праведзены перпендыкуляр)

{\displaystyle \ h_{b}}

$\{\displaystyle \ h_\{b\}\}$ — вышыня, праведзеная да стараны

{\displaystyle \ b}

$\{\displaystyle \ b\}$ , Гэтай формулай зручна карыстацца, калі можна лёгка знайсці вышыню.

Трыганаметрычны спосаб

Вышыню трохвугольніка можна вылічыць з выкарыстаннем трыганаметрычных формул. У адпаведнасці з абазначэннямі на выяве злева, вышыня роўная

= a sin ⁡ γ

{\displaystyle \ h_{b}=a\sin \gamma }

$\{\displaystyle \ h_\{b\}=a\sin \gamma \}$ . Калі падставіць вышыню ў формулу

S

1 2

{\displaystyle S={\frac {1}{2}}bh_{b}}

$\{\displaystyle S=\{\frac \{1\}\{2\}\}bh_\{b\}\}$ , атрымаем:

S

1 2

a b sin ⁡ γ

1 2

b c sin ⁡ α

1 2

c a sin ⁡ β .

{\displaystyle S={\frac {1}{2}}ab\sin \gamma ={\frac {1}{2}}bc\sin \alpha ={\frac {1}{2}}ca\sin \beta .}

$\{\displaystyle S=\{\frac \{1\}\{2\}\}ab\sin \gamma =\{\frac \{1\}\{2\}\}bc\sin \alpha =\{\frac \{1\}\{2\}\}ca\sin \beta .\}$ Акрамя таго,

sin ⁡ α

sin ⁡ ( π − α )

sin ⁡ ( β + γ ) ,

{\displaystyle \sin \alpha =\sin(\pi -\alpha )=\sin(\beta +\gamma ),}

$\{\displaystyle \sin \alpha =\sin(\pi -\alpha )=\sin(\beta +\gamma ),\}$ , што справядліва і для іншых двух вуглоў:

S

1 2

a b sin ⁡ ( α + β )

1 2

b c sin ⁡ ( β + γ )

1 2

c a sin ⁡ ( γ + α ) .

{\displaystyle S={\frac {1}{2}}ab\sin(\alpha +\beta )={\frac {1}{2}}bc\sin(\beta +\gamma )={\frac {1}{2}}ca\sin(\gamma +\alpha ).}

$\{\displaystyle S=\{\frac \{1\}\{2\}\}ab\sin(\alpha +\beta )=\{\frac \{1\}\{2\}\}bc\sin(\beta +\gamma )=\{\frac \{1\}\{2\}\}ca\sin(\gamma +\alpha ).\}$

З выкарыстаннем вектараў

Плошчу паралелаграма можна вылічыць з дапамогай вектараў. Няхай вектары AB і AC накіраваны адпаведна ад A да B і ад A да C. Тады плошча паралелаграма ABDC роўная |AB × AC|, г.зн. лікаваму значэнню вектарнага здабытка AB і AC. |AB × AC| роўны h · AC, дзе h — вышыня паралелаграма.

Плошча трохвугольніка ABC роўная палове плошчы паралелаграма S = ½|AB × AC|.

Плошчу трохвугольніка ABC таксама можна вылічыць як скалярны здабытак вектараў.

1 2

(

A B

⋅

A B

) (

A C

⋅

A C

) − (

A B

⋅

A C

)

1 2

A B

A C

− (

A B

⋅

A C

)

{\displaystyle {\frac {1}{2}}{\sqrt {(\mathbf {AB} \cdot \mathbf {AB} )(\mathbf {AC} \cdot \mathbf {AC} )-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}}={\frac {1}{2}}{\sqrt {|\mathbf {AB} |^{2}|\mathbf {AC} |^{2}-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}},.}

$\{\displaystyle \{\frac \{1\}\{2\}\}\{\sqrt \{(\mathbf \{AB\} \cdot \mathbf \{AB\} )(\mathbf \{AC\} \cdot \mathbf \{AC\} )-(\mathbf \{AB\} \cdot \mathbf \{AC\} )^\{2\}\}\}=\{\frac \{1\}\{2\}\}\{\sqrt \{|\mathbf \{AB\} |^\{2\}|\mathbf \{AC\} |^\{2\}-(\mathbf \{AB\} \cdot \mathbf \{AC\} )^\{2\}\}\}\,.\}$

Выкарыстанне каардынат

Калі пункт А размешчаны ў пункце пачатку адліку (0, 0) дэкартавай каардынатнай сістэмы, а каардынаты іншых двух пунктаў B = (xB, yB) і C = (xC, yC), тады плошчу S можна вылічыць як палавіну абсалютнага значэння вызначніка:

S

1 2

det

(

)

1 2

−

{\displaystyle S={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{B}&x_{C}\y_{B}&y_{C}\end{pmatrix}}\right|={\frac {1}{2}}|x_{B}y_{C}-x_{C}y_{B}|.}

$\{\displaystyle S=\{\frac \{1\}\{2\}\}\left|\det \{\begin\{pmatrix\}x_\{B\}&x_\{C\}\\y_\{B\}&y_\{C\}\end\{pmatrix\}\}\right|=\{\frac \{1\}\{2\}\}|x_\{B\}y_\{C\}-x_\{C\}y_\{B\}|.\}$ Ці ў агульным выпадку:

S

1 2

det

(

)

1 2

−

{\displaystyle S={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\y_{A}&y_{B}&y_{C}\1&1&1\end{pmatrix}}\right|={\frac {1}{2}}{\big |}x_{A}y_{C}-x_{A}y_{B}+x_{B}y_{A}-x_{B}y_{C}+x_{C}y_{B}-x_{C}y_{A}{\big |}.}

$\{\displaystyle S=\{\frac \{1\}\{2\}\}\left|\det \{\begin\{pmatrix\}x_\{A\}&x_\{B\}&x_\{C\}\\y_\{A\}&y_\{B\}&y_\{C\}\\1&1&1\end\{pmatrix\}\}\right|=\{\frac \{1\}\{2\}\}\{\big |\}x_\{A\}y_\{C\}-x_\{A\}y_\{B\}+x_\{B\}y_\{A\}-x_\{B\}y_\{C\}+x_\{C\}y_\{B\}-x_\{C\}y_\{A\}\{\big |\}.\}$ У трохмернай прасторы плошча трохвугольніка {A = (xA, yA, zA), B = (xB, yB, zB) і C = (xC, yC, zC)} роўная корню квадратнаму з сумы квадратаў адпаведных праекцый на тры галоўныя плоскасці (для якіх x = 0 або y = 0 або z = 0):

S

1 2

(

det

(

)

(

det

(

)

(

det

(

)

{\displaystyle S={\frac {1}{2}}{\sqrt {\left(\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\y_{A}&y_{B}&y_{C}\1&1&1\end{pmatrix}}\right)^{2}+\left(\det {\begin{pmatrix}y_{A}&y_{B}&y_{C}\z_{A}&z_{B}&z_{C}\1&1&1\end{pmatrix}}\right)^{2}+\left(\det {\begin{pmatrix}z_{A}&z_{B}&z_{C}\x_{A}&x_{B}&x_{C}\1&1&1\end{pmatrix}}\right)^{2}}}.}

$\{\displaystyle S=\{\frac \{1\}\{2\}\}\{\sqrt \{\left(\det \{\begin\{pmatrix\}x_\{A\}&x_\{B\}&x_\{C\}\\y_\{A\}&y_\{B\}&y_\{C\}\\1&1&1\end\{pmatrix\}\}\right)^\{2\}+\left(\det \{\begin\{pmatrix\}y_\{A\}&y_\{B\}&y_\{C\}\\z_\{A\}&z_\{B\}&z_\{C\}\\1&1&1\end\{pmatrix\}\}\right)^\{2\}+\left(\det \{\begin\{pmatrix\}z_\{A\}&z_\{B\}&z_\{C\}\\x_\{A\}&x_\{B\}&x_\{C\}\\1&1&1\end\{pmatrix\}\}\right)^\{2\}\}\}.\}$

Формула Герона

Форма трохвугольніка адназначна вызначаецца трыма старанамі. Адпаведна, для таго каб вылічыць плошчу дастаткова ведаць даўжыні старон. Паводле формулы Герона:

S

p ( p − a ) ( p − b ) ( p − c )

{\displaystyle S={\sqrt {p(p-a)(p-b)(p-c)}},}

$\{\displaystyle S=\{\sqrt \{p(p-a)(p-b)(p-c)\}\},\}$ дзе

p

a + b + c

{\displaystyle p={\frac {a+b+c}{2}}}

$\{\displaystyle p=\{\frac \{a+b+c\}\{2\}\}\}$ — паўперыметр. Іншы спосаб запісу формулы Герона:

S

1 4

(

)

− 2 (

)

{\displaystyle S={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}.}

$\{\displaystyle S=\{\frac \{1\}\{4\}\}\{\sqrt \{(a^\{2\}+b^\{2\}+c^\{2\})^\{2\}-2(a^\{4\}+b^\{4\}+c^\{4\})\}\}.\}$

Іншыя формулы

△ A B C

1 2

r ( a + b + c )

p r

( p − b )

{\displaystyle S_{\triangle ABC}={\frac {1}{2}}r(a+b+c)=pr=(p-b)r_{b}}

$\{\displaystyle S_\{\triangle ABC\}=\{\frac \{1\}\{2\}\}r(a+b+c)=pr=(p-b)r_\{b\}\}$ 2. S

△ A B C

a b c

4 R

{\displaystyle S_{\triangle ABC}={\frac {abc}{4R}}}

$\{\displaystyle S_\{\triangle ABC\}=\{\frac \{abc\}\{4R\}\}\}$ 3. S

△ A B C

sin ⁡ β sin ⁡ γ

2 sin ⁡ α

{\displaystyle S_{\triangle ABC}={\frac {a^{2}\sin \beta \sin \gamma }{2\sin \alpha }}}

$\{\displaystyle S_\{\triangle ABC\}=\{\frac \{a^\{2\}\sin \beta \sin \gamma \}\{2\sin \alpha \}\}\}$ 4. S

△ A B C

sin ⁡ α sin ⁡ β sin ⁡ γ

{\displaystyle S_{\triangle ABC}={2R^{2}\sin \alpha \sin \beta \sin \gamma }}

$\{\displaystyle S_\{\triangle ABC\}=\{2R^\{2\}\sin \alpha \sin \beta \sin \gamma \}\}$ 5. S

△ A B C

1 2

[

(

−

) +

(

−

) +

(

−

) ]

{\displaystyle S_{\triangle ABC}={\frac {1}{2}}[x_{A}(y_{B}-y_{C})+x_{B}(y_{C}-y_{A})+x_{C}(y_{A}-y_{B})]}

$\{\displaystyle S_\{\triangle ABC\}=\{\frac \{1\}\{2\}\}[x_\{A\}(y_\{B\}-y_\{C\})+x_\{B\}(y_\{C\}-y_\{A\})+x_\{C\}(y_\{A\}-y_\{B\})]\}$ у дадзенай формуле варта звярнуць увагу на абход вяршынь, калі йсці па гадзіннікавай стрэлцы, то атрымаецца тая ж плошча, але з адмоўным знакам 6. S