wd wp Пошук: ⬜

Аксіёма паралельнасці Еўкліда

Аксіё́ма парале́льнасці Еўклі́да, або пя́ты пастула́т — адна з аксіём класічнай планіметрыі. Упершыню прыведзена ў «Пачатках» Еўкліда [1]:

І калі прамая, падаючы на дзве прамыя, утварае ўнутраныя і па адзін бок вуглы, меншыя за два прамыя, то працягнутыя неабмежавана гэтыя прамыя сустрэнуцца з таго боку, дзе вуглы меншыя за два прамыя.

Арыгінальны тэкст (стар.-грэч.)

Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ' ἄπειρον συμπίπτειν, ἐφ' ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες.

— ΣTOIXEIA EΥKΛEI∆OΥ

Еўклід адрознівае паняцці пастулат і аксіёма, не тлумачачы іх розніцы; у розных рукапісах «Пачаткаў» Еўкліда раздзяленне сцвярджэнняў на аксіёмы і пастулаты адрозніваецца, таксама не супадае і іх парадак. У класічным выданні «Пачаткаў» Хейберга сфармуляванае сцвярджэнне з’яўляецца пятым пастулатам.

На сучаснай мове Еўклідаў тэкст можна перафармуляваць так[2]:

Калі [на плоскасці] пры перасячэнні дзвюх прамых трэцяю сума ўнутраных аднабаковых вуглоў меншая за 180°, то гэтыя прамыя пры дастатковым прадаўжэнні перасякаюцца, і прытым з таго боку, з якое гэта сума меншая за 180°.

Удакладненне, з якога іменна боку перасякаюцца прамыя, Еўклід дадаў, верагодна, дзеля яснасці — лёгка даказаць, што яно выцякае з самога факта існавання перасячэння[2].

Пяты пастулат вельмі моцна вылучаецца сярод іншых пастулатаў Еўкліда, простых і інтуітыўна відавочных (гл. Пачаткі Еўкліда). Таму на працягу двух тысячагоддзяў не спыняліся спробы выключыць яго са спіса аксіём і вывесці як тэарэму. Усе гэтыя спробы закончыліся няўдачаю. «Верагодна, немагчыма ў навуцы знайсці больш захапляльную і драматычную гісторыю, чым гісторыя пятага пастулата Еўкліда»[3]. Нягледзячы на адмоўны вынік, гэтыя пошукі не былі дарэмнымі, бо ў канчатковым выніку прывялі да поўнага перагляду навуковых уяўленняў аб геаметрыі Сусвету.

Эквівалентныя фармулёўкі пастулата аб паралельных

У сучасных крыніцах звычайна прыводзіцца іншая фармулёўка пастулата аб паралельных, раўназначная V пастулату. Яна належыць Проклу [4] (у замежнай літаратуры яе часта называюць аксіёмаю Плейфера):

На плоскасці праз пункт, які не ляжыць на дадзенай прамой, можна правесці адну і толькі адну прамую, паралельную дадзенай.

У гэтай фармулёўцы слова «адну і толькі адну» часта замяняюць на «толькі адну» ці «не больш чым адну», бо існаванне хаця б аднае такой паралельнай адразу вынікае з тэарэм 27 і 28 «Пачаткаў» Еўкліда.

Увогуле, для V пастулата існуе вялікая колькасць раўназначных фармулёвак, многія з якіх самі па сабе здаюцца даволі відавочнымі. Вот некаторыя з іх[5][6][7].

Існуе прамавугольнік (хаця б адзін), г. зн. чатырохвугольнік, у якога ўсе вуглы прамыя[8].
Існуюць падобныя, але не роўныя трохвугольнікі (аксіёма Валіса, 1693). І тут дастаткова, каб існавала хоць адна пара такіх трохвугольнікаў[8].
Любую фігуру можна прапарцыянальна павялічыць.
- Варыянт: ёсць хоць адна фігура, якую можна прапарцыянальна павялічыць.
Існуе трохвугольнік з адвольна вялікаю плошчаю.
Прамая, праведзеная праз пункт унутры вугла, перасякае прынамсі адну яго старану (аксіёма Іагана Фрыдрыха Лорэнца, 1791).
Праз кожны пункт унутры вострага вугла заўсёды можна правесці прамую так, каб яна перасякала абедзве яго стараны (адно з дапушчэнняў Лежандра, 1800).
Прамыя, збліжаючыся, рана ці позна перасякуцца.
- Варыянт: перпендыкуляр і нахільная да аднае і тае ж прамой абавязкова перасякаюцца. Сцвярджэнне вядомае як пастулат Лежандра, хоць гэта фармулёўка сустракалася яшчэ ў XIII стагоддзі ў працах ат-Тусі.
Пункты, роўнааддаленыя ад данай прамой (па адзін бок), утвараюць прамую.
- Варыянт: адлегласць паміж паралельнымі прамымі заўсёды нязменная, г. зн. паралельныя прамыя не могуць ні збліжацца, ні разбягацца.
Калі дзве прамыя пачалі збліжацца, то немагчыма, каб яны затым пачалі (у той жа бок, без перасячэння) разбягацца (аксіёма Роберта Сімсана, 1756).
- Варыянт: Калі дзве прамыя ў адзін бок разбягаюцца, то ў другі — збліжаюцца.
Сума вуглоў аднолькавая ва ўсіх трохвугольнікаў.
- Варыянт: існуе хоць адна пара нероўнавялікіх трохвугольнікаў з аднолькаваю сумаю вуглоў.
Існуе трохвугольнік (хоць адзін), сума вуглоў якога роўна двум прамым[8].
Дзве прамыя, паралельныя трэцяй, паралельныя і адна адной (аксіёма Астраградскага, 1855).
Лінія, артаганальная некатораму сямейству паралельных прамых, ёсць прамая.
Прамая, перасякаючы адну з паралельных прамых, абавязкова перасячэ і другую.
Для ўсякага нявыраджанага трохвугольніка існуе апісаная акружнасць (аксіёма Форкаша Бояі).
Справядліва тэарэма Піфагора (хаця б для аднаго прамовугольнага трохвугольніка).
- Варыянт: прастора мае Еўклідаву метрыку.
Адносіна даўжыні акружнасці да яе дыяметра ёсць пастаянная велічыня, г. зн. аднолькавая для любой акружнасці.
- Варыянт: дзель даўжыні акружнасці на яе дыяметр роўная ліку Пі (хаця б у аднае акружнасці).

Іх раўназначнасць азначае, што іх усе можна даказаць як тэарэмы, калі прыняць V пастулат, і наадварот, замяняючы V пастулат на любое з гэтых сцвярджэнняў, можна даказаць зыходны V пастулат як тэарэму.

Калі замест V пастулата дапусціць, што для пары пункт—прамая V пастулат несправядлівы, то атрыманая сістэма аксіём будзе апісваць геаметрыю Лабачэўскага. Зразумела, што ў геаметрыі Лабачэўскага ўсе вышэйназваныя раўназначныя сцвярджэнні не спраўджваюцца.

Сістэма аксіём сферычнай геаметрыі таксама патрабуе змянення і іншых аксіём Еўкліда[9].

Пяты пастулат рэзка выдзяляецца сярод іншых, даволі відавочных, ён больш падобен на складаную, невідавочную тэарэму. Еўклід, верагодна, усведамляў гэта, і таму першыя 28 сцвярджэнняў у «Пачатках» даказваюцца без яго дапамогі.

«Еўклід безумоўна павінен быў ведаць розныя формы пастулата аб паралельных»[4]. Чаму ж ён выбраў прыведзеную, складаную і грувасткую? Гісторыкі выказвалі розныя меркаванні аб прычынах такога выбару. В. П. Смілга меркаваў, што Еўклід такой фармулёўкай паказваў, што гэтая частка тэорыі незавершана[10]. М. Клайн звяртае ўвагу на тое, што Еўклідаў пяты пастулат мае лакальны характар, г. зн. апісвае з’яву на абмежаваным участку плоскасці, тады як, напрыклад, аксіёма Прокла сцвярджае факт паралельнасці, які патрабуе разгляду ўсяе бесканечнай прамой[11]. Трэба патлумачыць, што антычныя матэматыкі пазбягалі выкарыстання актуальнай бесканечнасці; напрыклад, дургі пастулат Еўкліда сцвярджае не бесканечнасць прамой, а ўсяго толькі тое, што «прамую можна непарыўна працягваць». З пункту погляду антычных матэматыкаў, вышэйназваныя эквіваленты пастулата аб паралельных маглі казацца непрымальнымі: яны альбо спасылаюцца на актуальную бесканечнасць ці (яшчэ не ўведзенае) паняцце вымярэння, альбо таксама не вельмі відавочныя. Яшчэ адну версію прапанаваў гісторык Імрэ Тот[12]: еўклідава фармулёўка, магчыма, была спачатку (памылкова даказанаю) тэарэмаю ў кагосьці з папярэднікаў Еўкліда, і калі пераканаліся, што даказаць яе не ўдаецца, статус тэарэмы павысілі да пастулата, не мяняючы тэксту фармулёўкі.

Абсалютная геаметрыя

Асноўны артыкул: Абсалютная геаметрыя Калі са спіса аксіём выключыць V пастулат, то атрыманая сістэма аксіём будзе апісваць так званую абсалютную геаметрыю. У прыватнасці, першыя 28 тэарэм «Пачаткаў» Еўкліда даказваюцца без выкарыстання V пастулата і таму адносяцца да абсалютнай геаметрыі. Для далейшага адзначым дзве тэарэмы абсалютнай геаметрыі:

Паралельныя прамыя існуюць; гэта вынікае з тэарэм 27 і 28 «Пачаткаў» Еўкліда.
Пры прадаўжэнні дзвюх прамых ад пункта іх перасячэння адлегласць паміж імі неабмежавана нарастае[13].

Спробы доказу

Матэматыкі з даўніх часоў спрабавалі «палепшыць Еўкліда» — альбо выключыць пяты пастулат з ліку зыходных сцвярджэнняў, г. зн. даказаць яго, абапіраючыся на астатнія пастулаты і аксіёмы, альбо замяніць яго іншым, такім жа відавочным, як іншыя пастулаты. Надзею на дасяжнасць гэтага выніку патрымлівала тое, што IV пастулат Еўкліда (усе прамые вуглы роўныя між сабой) і праўда аказаўся лішнім — ён быў строга даказан як тэарэма і выключаны з пераліку аксіём[5].

За два тысячагоддзі было прапанавана шмат доказаў пятага пастулата, але ў кожным з іх рана ці позна выяўляўся заганны круг: аказвалася, што сярод яўных ці няяўных дапушчэнняў было сцвярджэнне, якое не ўдаецца даказаць без выкарыстання таго ж пятага пастулата.

Прокл (V стагоддзе н. э.) у «Каментарыі да I кнігі Пачаткаў Еўкліда» паведамляе, што такі доказ прапанаваў Клаўдзій Пталемей, крытыкуе яго доказ і прапануе свой уласны[13]. Спрошчана яго можна апісаць так: няхай прамая

{\displaystyle b}

$\{\displaystyle b\}$ праходзіць праз вызначаны пункт

{\displaystyle A}

$\{\displaystyle A\}$ паралельна прамой

{\displaystyle a}

$\{\displaystyle a\}$ ; дакажам, што любая іншая прамая

{\displaystyle c}

$\{\displaystyle c\}$ , праведзеная праз той жа пункт, перасякаецца з прамою

{\displaystyle a}

$\{\displaystyle a\}$ . Як гаварылася вышэй, адлегласць паміж прамымі ад пункта іх перасячэння нарастае неабмежаванна (яшчэ раз падкрэслім, што доказ гэтай тэарэмы не абапіраецца на V пастулат). Але тады ў рэшце рэшт адлегласць паміж

{\displaystyle c}

$\{\displaystyle c\}$ і

{\displaystyle b}

$\{\displaystyle b\}$ перавысіць адлегласць паміж паралельнымі прамымі, г. зн. прамыя

{\displaystyle c}

$\{\displaystyle c\}$ і

{\displaystyle a}

$\{\displaystyle a\}$ перасякуцца.

Прыведзены доказ апіраецца на дапушчэнне, што адлегласць паміж прамымі пастаянная (ці хаця б абмежавана). Пазней высветлілася, што гэтае дапушчэнне раўназначнае V пастулату.

Вучоны I стагоддзя да н. э. Пасідоній прапанаваў вызначыць паралельные як прамыя, на ўсём працягу роўнааддаленыя адна ад аднае. З такога азначэння лёгка выводзіцца пяты пастулат. Аднак Пасідоніева азначэнне некарэктнае: ніадкуль не вынікае, што лінія, роўнааддаленая ад данай прамой, ёсць прамая[14].

Пасля ўпадку антычнае культуры V пастулатам заняліся матэматыкі ісламскіх краін. Доказ ал-Джаухары, вучня ал-Харэзмі (IX стагоддзе)[15], няяўна дапускаў, што калі пры перасячэнні дзвюх прамых нейкаю трэцяю накрыж-ляжачыя вуглы роўныя, то тое ж справядліва пры перасячэнні тых жа прамых любою іншаю. І гэта дапушчэнне раўназначнае V пастулату.

Сабіт ібн Кура (IX стагоддзе) даў два доказы; у першым ён апіраецца на дапушчэнне, што калі дзве прамыя аддаляюцца адна ад аднае з аднаго боку, яны абавязкова прыбліжаюцца з другога боку. У другім, як і Пасідоній, ён зыходзіць з існавання роўнааддаленых прамых, прычом гэты факт ібн Кура спрабуе вывесці з уяўлення аб «простым руху», г. зн. аб раўнамерным руху на нязменнай адлегласці ад прамой (яму здаецца відавочным, што траекторыя такога руху — таксама прамая)[16]. Кожнае з двух названых сцвярджэнняў Ібн Куры раўназначнае V пастулату.

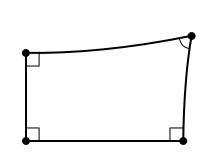
Падобную ж памылку зрабіў ібн ал-Хайсам, але ён упершыню разгледзеў фігуру, якую пазней сталі называць «чатырохвугольнікам Ламберта», — чатырохвугольнік, у якога тры ўнутраныя вуглы — прамыя. Ён сфармуляваў тры магчымыя варыянты для чацвёртага вугла: востры, прамы, тупы. Абмеркаванне гэтых трох гіпотэз, у розных варыянтах, шмат разоў узнікала ў пазнейшых даследаваннях.

Паэт і матэматык Амар Хаям раскрытыкаваў спробы ўвесці ў геаметрыю механічны рух. Ён прапанаваў замяніць V пастулат на іншы, больш просты: дзве прамыя, збягаючыся, перасякаюцца, і немагчыма, каб дзве прамыя разбягаліся ў напрамку збліжэння. Кожная з дзвюх частак гэтага сцвярджэння раўназначная пастулату Еўкліда[17].

Ал-Абхары прапанаваў доказ, падобны да доказу ал-Джаухары. (Гэты доказ прыводзіць у сваёй кнізе ас-Самаркандзі, і рад даследчыкаў лічыў яго доказам ас-Самаркандзі.) Ён зыходзіць з вернага ў абсалютнай геаметрыі сцвярджэння, што для ўсякай прамой, якая перасякае стораны данага вугла, можна пабудаваць яшчэ адну прамую, якая перасякае стораны гэтага ж вугла і ляжыць ад яго вяршыні далей, чым першая. Але з гэтага сцвярджэння ён робіць неабгрунтаваны вывад, што праз усякі пункт унутры данага вугла можна правесці прамую так, каб яна перасякала абедзве стораны гэтага вугла, — і будуе на апошнім сцвярджэнні, раўназначным V пастулату, увесь далейшы доказ.

Насір ад-Дзін ат-Тусі прапанаваў пабудову, падобную на пабудову Амара Хаяма [18]. Адзначым, што творы ат-Тусі сталі вядомыя Джону Валісу, і тым самым адыгралі ролю ў разгортванні даследаванняў па нееўклідавай геаметрыі ў Еўропе.

У сярэдневяковай Еўропе першую вядомую спробу доказу аксіёмы паралельнасці Еўкліда зрабіў жыхар Праванса (Францыя) Герсанід (ён жа Леві бен Гершом, XIV стагоддзе). Яго доказ апіраўся на сцвярджэнне аб існаванні прамавугольніка [19].

Да XVI стагоддзя адносіцца доказ вучонага-езуіта Хрыстафора Клавіуса. Яго доказ, як і ў ібн Куры, быў заснаваны на сцвярджэнні, што лінія, роўнааддаленая ад прамой — таксама прамая[20].

Валіс у 1693 годзе ў адной са сваіх прац прыводзіць пераклад твора ат-Тусі і прапануе раўназначную, але больш простую фармулёўку: існуюць падобныя, але не роўныя фігуры[21]. Клеро ў сваіх «Пачатках геаметрыі» (1741), як і Герсанід, замест V пастулата ўзяў яго эквівалент «існуе прамавугольнік».

У целым можна сказаць, што ўсе пералічаныя спробы прынеслі немалую карысць: была ўстаноўлена сувязь паміж V пастулатам і іншымі сцвярджэннямі, былі выразна сфармуляваны дзве альтэрнатывы V пастулату — гіпотэзы вострага і тупога вугла.

Першыя накіды нееўклідавай геаметрыі

Глыбокае даследаванне V пастулата, заснаванае на цалкам арыгінальным прынцыпе, правёў у 1733 годзе італьянскі манах-езуіт, выкладчык матэматыкі Джыралама Сакеры. Ён апублікаваў працу пад назваю «Еўклід, ачышчаны ад усіх плям, альбо геаметрычная спроба ўстанавіць самыя першыя пачаткі ўсяе геаметрыі». Ідэя Сакеры заключалася ў тым, каб замяніць V пастулат процілеглым сцвярджэннем, вывесці з новай сістэмы аксіём як мага больш вынікаў, тым самым пабудаваўшы «ілжывую геаметрыю», і знайсці ў гэтай геаметрыі супярэчнасці ці яўна непрымальныя вывады. Тады справядлівасць V пастулата будзе даказана ад процілеглага [22].

Сакеры разглядае ўсё тыя ж тры гіпотэзы аб 4-м вугле чатырохвугольніка Ламберта. Гіпотэзу тупога вугла ён адкінуў адразу з фармальных меркаванняў. Лёгка паказаць, што ў гэтым выпадку наогул усе прамыя перасякаюцца, а тады атрымліваецца, што V пастулат Еўкліда справядлівы — бо ён як-раз і сцвярджае, што пры некаторых умовах прамыя перасякаюцца. Адсюль робіцца вывад, што «гіпотэза тупога вугла заўсёды цалкам няслушная, бо яна сама сябе разбурае»[23].

Пасля гэтага Сакеры пераходзіць да абвяржэння «гіпотэзы вострага вугла», і тут яго даследаванне значна цікавейшае. Ён дапускае, што яна справядлівая, і, адзін за адным, даказвае рад вынікаў. Сам таго не падазраваючы, ён прасоўваецца даволі далёка ў пабудове геаметрыі Лабачэўскага. Многія тэарэмы, даказаныя Сакеры, выглядаюць інтуітыўна непрымальнымі, але ён працягвае ланцужок тэарэм. Нарэшце, Сакеры даказвае, што ў «ілжывай геаметрыі» любые дзве прамыя ці перасякаюцца, ці маюць агульны перпендыкуляр, па абодва бакі ад якога яны аддаляюцца адна ад аднае, ці аддаляюцца адна ад аднае з аднаго боку і неабмежавана збліжаюцца з другога. У гэтым месцы Сакеры робіць нечаканы вывад: «гіпотэза вострага вугла цалкам няслушная, бо супярэчыць прыродзе прамой лініі»[24].

Відаць, Сакеры адчуваў неабгрунтаванасць гэтага «доказу», бо даследаванне працягваецца. Ён разглядае эквідыстанту — геаметрычнае месца пунктаў плоскасці, роўнааддаленых ад прамой; у адрозненне ад сваіх папярэднікаў, Сакеры разумее, што ў даным выпадку гэта зусім не прамая. Аднак, вылічваючы даўжыню яе дугі, Сакеры дапускае памылку і прыходзіць к сапраўднай супярэчнасці, пасля чаго заканчвае даследаванне і з палёгкаю заяўляе, што ён «вырваў гэту злашкодную гіпотэзу з коранем». На жаль, піянерская праца Сакеры, выдадзеная пасмяротна, не прыцягнула да сябе тае ўвагі матэматыкаў, якой заслугоўвала, і толькі праз 150 год (1889) яго суайчыннік Бельтрамі знайшоў гэту забытую працу і ацаніў яе гістарычнае значэнне.

У другой палавіне XVIII стагоддзя было апублікавана больш чым 50 прац па тэорыі паралельных. У аглядзе тых гадоў (Г. С. Клюгель) даследуецца больш чым 30 спроб даказаць V пастулат і даказваецца іх памылковасць. Вядомы нямецкі матэматык і фізік І. Г. Ламберт, з якім Клюгель перапісваўся, таксама зацікавіўся праблемаю; яго «Тэорыя паралельных ліній» была выдадзена (як і праца Сакеры, пасмяротна) у 1786 годзе.

Сферычная геаметрыя: усе прамыя перасякаюцца

Ламберт першы ўстанавіў, што «геаметрыя тупога вугла» рэалізуецца на сферы, калі пад прамымі разумець вялікія кругі. Ён, як і Сакеры, вывеў з «гіпотэзы вострага вугла» мноства вынікаў, прычым прасунуўся значна далей за Сакеры; сярод іншага, ён устанавіў, што дапаўненне сумы вуглоў трохвугольніка да 180° прапарцыянальнае плошчы трохвугольніка.

У сваёй кнізе Ламберт пранікліва заўважыў[25]:

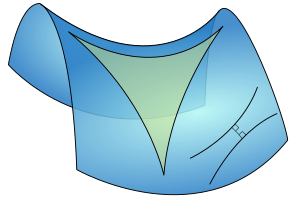
Мне здаецца вельмі выдатным, што другая гіпотэза [тупога вугла] спраўджваецца, калі замест плоскіх трохвугольнікаў узяць сферычныя. Я з гэтага амаль павінен быў бы зрабіць вывад — заключэнне, што трэцяя гіпотэза мае месца на нейкай уяўнай сферы. Ва ўсякім разе, павінна ж быць прычына, чаму яна на плоскасці не так лёгка паддаецца абвяржэнню, як гэта магло быць зроблена ў адносінах другой гіпотэзы.

Ламберт не знайшоў супярэчнасці ў гіпотэзе вострага вугла і прыйшоў к заключэнню, што ўсе спробы даказаць V пастулат безнадзейныя. Ён не выказаў якіх-небудзь сумненняў у няслушнасці «геаметрыі вострага вугла», аднак, судзячы па другой яго праніклівай заўвазе, Ламберт думаў аб магчымай фізічнай рэальнасці нееўклідавай геаметрыі і аб выніках гэтага для навукі[26]:

У гэтым ёсць нешта цудоўнае, што выклікае жаданне, каб трэцяя гіпотэза была справядлівая. І ўсё ж я хацеў бы <…>, каб гэта было не так, бо гэта было б спалучана з цэлым радам <…> нязручнасцей. Трыганаметрычныя табліцы сталі б бясконца вялізнымі, падобнасць і прапарцыянальнасць фігур не існавалі б зусім <…>, астраноміі прыйшлося б дрэнна.

Выдатная праца Ламберта, як і кніга Сакеры, далёка апярэдзіла свой час і выклікала цікавасці ў тагачасных матэматыкаў. Тая ж доля спасцігла «астральную геаметрыю» нямецкіх матэматыкаў Ф. К. Швайкарта (1817) і Ф. А. Таурынуса (1826), па ідэях блізкую да пабудаванай Ламбертам.

Тым часам спробы «змыць плямы» з Еўкліда працягваліся (Луі Бертран, Лежандр, Сямён Гур’еў і іншыя). Лежандр даў цэлых тры доказы V пастулата, памылковасць якіх скора паказалі яго сучаснікі[27]. Апошні «доказ» ён апублікаваў у 1823 годзе, за тры гады да першага дакладу Лабачэўскага аб новай геаметрыі.

Адкрыццё нееўклідавай геаметрыі

У першай палавіне XIX стагоддзя па шляху, пракладзенаму Сакеры, пайшлі К. Ф. Гаус, Я. Бояі, М. І. Лабачэўскі і Ф. К. Швайкарт. Але мэта ў іх была ўжо іншая — не выкрыць нееўклідаву геаметрыю як немагчымую, а, наадварот, пабудаваць альтэрнатыўную геаметрыю і высветліць яе магчымую ролю ў рэальным свеце. На той момант гэта была цалкам ератычная ідэя; ніхто з вучоных раней не сумняваўся, што фізічная прастора еўклідава. Цікава, што Гауса і Лабачэўскага вучыў у маладосці адзін настаўнік — Марцін Бартэльс, які, зрэшты, сам нееўклідавай геаметрыяй не займаўся.

Першым быў Швайкарт. У 1818 годзе ён адправіў Гаусу пісьмо з сур’ёзным аналізам асноў нееўклідавай геаметрыі, аднак устрымаўся ад вынясення сваіх поглядаў на публічнае абмеркаванне. Гаус таксама не адважыўся апублікаваць працу на гэту тэму, але яго чарнавыя заметкі і некалькі пісем адназначна пацвярджаюць глыбокае разуменне нееўклідавай геаметрыі. Вот некалькі характэрных урыўкаў з пісем Гауса, дзе ўпершыню ў навуцы паяўляецца тэрмін «нееўклідава геаметрыя»[28]:

Дапушчэнне, што сума трох вуглоў трохвугольніка меншая за 180°, прыводзіць да своеасаблівай, цалкам непадобнай на нашу [еўклідаву] геаметрыі; гэта геаметрыя цалкам паслядоўная, і я развіў яе для сябе цалкам задавальняюча; я маю магчымасць рашыць у гэтай геаметрыі любую задачу, за выключэннем вызначэння некаторац пастаяннай^[29], значэнне якой a priori ўстаноўлена быць не можа.

Чым большае значэнне мы нададзім гэтай сталай, тым бліжэй мы падыдзем к еўклідавай геаметрыі, а бесканечна вялікае яе значэнне прыводзіць абедзве сістэмы к супадзенню. Сцвярджэнні гэтай геаметрыі часткова здаюцца парадаксальнымі і непрывычнаму чалавеку нават недарэчнымі; але пры строгім і спакойным разважанні аказваецца, што яны не ўтрымліваюць нічога немагчымага. Так, напрыклад, усе тры вуглы трохвугольніка можна зрабіць адвольна малымі, калі толькі ўзяць дастаткова вялікія стораны; плошча ж трохвугольніка не можа перавысіць, нават не можа дасягнуць некаторай граніцы, якімі б вялікімі ні былі яго стораны. Усе мае старанні знайсці ў гэтай нееўклідавай геаметрыі супярэчнасць ці непаслядоўнасць засталіся безвыніковымі, і адзінае, што ў гэтай сістэме працівіцца нашаму розуму, гэта тое, што ў прасторы, калі б гэта сістэма была справядліва, павінна была б існаваць некаторая сама па сабе вызначаная (хоць нам і невядомая) лінейная велічыня. Але мне здаецца, што мы, акрамя бяззместавай славеснай мудрасці метафізікаў, знаем вельмі мала ці нават не знаем нічога пра сутнасць прасторы. (З пісьма Таурынусу, 1824)

У 1818 годзе ў пісьме аўстрыйскаму астраному Герлінгу Гаус выказаў свае асцярогі[30]:

Я радуюся, што Вы маеце мужнасць выказацца так, як калі б Вы прызнавалі няслушнасць нашай тэорыі паралельных, а разам з тым і ўсяе нашай геаметрыі. Але восы, чыё гняздо Вы патрывожыце, паляцяць Вам на галаву.

Азнаёміўшыся з працаю Лабачэўскага «Геаметрычныя даследаванні па тэорыі паралельных», Гаус энергічна хадатайнічае аб абранні рускага матэматыка замежным членам-карэспандэнтам Гётынгенскага каралеўскага таварыства (што і адбылося ў 1842 годзе).

Лабачэўскі і Бояі праявілі большую смеласць, чым Гаус, і амаль адначасова (Лабачэўскі — у дакладзе 1826 года і публікацыі 1829 года; Бояі — у пісьме 1831 года і публікацыі 1832 года), незалежна адзін ад другога, апублікавалі выклад таго, што цяпер называецца геаметрыяй Лабачэўскага. Лабачэўскі прасунуўся ў даследаванні новай геаметрыі далей за ўсіх, і яна сёння носіць яго імя. Але галоўная яго заслуга не ў гэтым, а ў тым, што ён паверыў у новую геаметрыю і меў мужнасць адстойваць сваё перакананне (ён нават прапанаваў эксперыментальна праверыць V пастулат, вымерыўшы суму вуглоў трохвугольніка)[31].

Ва ўступленні да сваёй кнігі «Новые начала геометрии» Лабачэўскі рашуча заяўляе[32]:

Усім вядома, што ў геаметрыі тэорыя паралельных дагэтуль заставалася недасканалаю. Дарэмныя старанні з часоў Еўкліда, на працягу дзвюх тысяч год, прымусілі мяне падазраваць, што ў саміх паняццях яшчэ не заключаецца тае ісціны, якую хацелі даказваць і якую праверыць, як і іншыя фізічныя законы, могуць толькі вопыты, як, напрыклад, астранамічныя назіранні. <…> Галоўнае заключэнне <…> дапускае існаванне геаметрыі ў шырэйшым сэнсе, чым яе прадставіў нам першы Еўклід. У гэтым шырокім выглядзе даў я навуцы назву Уяўнай Геаметрыі, куды, як асобны выпадак, уваходзіць Ужывальная Геаметрыя.

Арыгінальны тэкст (руск.)

Всем известно, что в геометрии теория параллельных до сих пор оставалась несовершенной. Напрасное старание со времён Евклида, в продолжении двух тысяч лет, заставили меня подозревать, что в самых понятиях ещё не заключается той истины, которую хотели доказывать и которую проверить, подобно другим физическим законам, могут лишь опыты, каковы, например, астрономические наблюдения.<…> Главное заключение <…> допускает существование геометрии в более обширном смысле, нежели как ее представил нам первый Евклид. В этом пространном виде дал я науке название Воображаемой Геометрии, где как частный случай входит Употребительная Геометрия.

Трагічная доля Лабачэўскага, падвергнутага астракізму ў навуковым свеце і службовым асяроддзі за занадта смелыя мыслі, паказала, што асцярогі Гауса былі не дарэмныя. Але і яго барацьба была не дарэмная. Па іроніі лёсу перамогу смелых ідэй Лабачэўскага забяспечыў (пасмяротна) асцярожны Гаус. У 1860-я годы была апублікавана перапіска Гауса, у тым ліку некалькі захопленых водгукаў аб геаметрыі Лабачэўскага, і гэта прыцягнула ўвагу к працам рускага матэматыка. У 1868 годзе выходзіць артыкул Э. Бельтрамі, які паказаў, што плоскасць Лабачэўскага мае пастаянную адмоўную крывізну (у еўклідавай плоскасці крывізна нулявая, у сферы — дадатная); вельмі скора нееўклідава геаметрыя набыла статус законнай навукі, хоць усё яшчэ разглядалася як чыста адцягнутая (абстрактная).

У канцы XIX—пачатку XX стагоддзя спачатку матэматыкі (Бернхард Рыман, Уільям Кінгдан Кліфард), а затым і фізікі (Агульная тэорыя адноснасці, Эйнштэйн), канчаткова пакончылі з дагматам аб еўклідавай геаметрыі фізічнай прасторы.

Доказ незалежнасці пятага пастулата

Даказаць несупярэчлівасць новай геаметрыі ні Лабачэўскі, ні Бояі не змаглі — тады матэматыка яшчэ не мела неабходных для гэтага сродкаў. Толькі праз 40 год з’явілася мадэль Клейна (1871) і мадэль Пуанкарэ (1882), у якіх рэалізавана аксіяматыка геаметрыі Лабачэўскага на аснове еўклідавай геаметрыі. Гэтыя мадэлі пераканаўча даказваюць, што адмаўленне V пастулата не супярэчыць астатнім аксіёмам геаметрыі; адсюль выцякае, што V пастулат не залежыць ад астатніх аксіём, і даказаць яго немагчыма.

Зноскі

↑ Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948. — Т. I. — С. 15.
1 2 Каган. Лобачевский, 1948, с. 164-165
↑ Смилга, 1988, с. 4
1 2 История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 110.
1 2 Мордухай-Болтовской Д. Д. Комментарии к «Началам» Евклида, книги I-VI. Указ. соч. — С. 241-244.
↑ Euclid’s Fifth Postulate
↑ Каган. Лобачевский, 1948, с. 167-175
1 2 3 Лелон-Ферран Ж., 1989, с. 255-256.
↑ Joel Castellanos.. Non-Euclid. Axioms and Theorems(англ.) (недаступная спасылка). Архівавана з першакрыніцы 6 верасня 2013. Праверана 11 февраля 2010.
↑ Смилга, 1988, с. 59-61
↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 169.
↑ Tóth I. Das Parallelenproblem im Corpus Aristotelicum // Archive for history of exact sciences. — Berlin—Heidelberg—New York: 1967. — В. 4,5. — Т. 3. — С. 249-422.
1 2 Смилга, 1988, с. 72
↑ Лаптев Б. Л. Н. И. Лобачевский и его геометрия. — М.: Просвещение, 1976. — С. 71. — 112 с.
↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 231.
↑ Ибн Корра. Книга о том, что две линии, проведённые под углом, меньшим двух прямых, встречаются / Перевод и примечания Б. А. Розенфельда. — М.: ИМИ, 1963. — Т. XV. — С. 363—380.
↑ Хаййам. Трактаты / Перевод Б. А. Розенфельда. Редакция В. С. Сегаля и А. П. Юшкевича. Статья и комментарии Б. А. Розенфельда и А. П. Юшкевича. — М., 1962.
↑ Ат-Туси. Трактат, исцеляющий сомнение по поводу параллельных линий / Перевод Б. А. Розенфельда, примечания Б. А. Розенфельда и А. П. Юшкевича. — М.: ИМИ, 1960. — Т. XIII. — С. 483—532.
↑ Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
↑ Clavius C. Euclidis Elementorum, libri XV. — Romae, 1574.
↑ Wallis. Opera mathematica, v. II. — Oxoniae, 1693. — С. 665.
↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 215-217.
↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 100.
↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 105.
↑ Lambert J. H. Deutscher Gelehrter Briefwechsel. Bd. 1-5. Herausg. von J. Bernoulli. — Berlin, 1781—1784. — С. 202—203.
↑ Смилга, 1988, с. 121
↑ История математики, том III, стр. 218.
↑ Об основаниях геометрии, стр. 101-120.
↑ З іншага пісьма вынікае, што пастаянная раўняецца

− k

{\displaystyle 1/{\sqrt {-k}}}

$\{\displaystyle 1/\{\sqrt \{-k\}\}\}$ , дзе

{\displaystyle k}

$\{\displaystyle k\}$ абазначае крывізну. 30. ↑ Об основаниях геометрии, с. 119—120. 31. ↑ Лобачевский Н. И. Сочинения по геометрии (Полн. собр. соч., тт. 1—3). — М. — Л.: ГИТТЛ, 1946—1949. 32. ↑ Об основаниях геометрии, с. 61-62.

Літаратура

Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948.
- Тэкст кніг I—VI на www.math.ru ці на mccme.ru Архівавана 11 жніўня 2011. (руск.)
Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — 468 с.
Гильберт Д. Основания геометрии. — Л.: Сеятель, 1923. — 152 с.
История математики с древнейших времён до начала XIX столетия. — М.: Наука, 1972.
Каган В. Ф. Геометрия Лобачевского и её предыстория. — М.—Л., 1949.
Каган В. Ф. Лобачевский. — Издание второе, дополненное. — М.-Л.: АН СССР, 1948. — 507 с.
Лелон-Ферран Ж. Основания геометрии. — М.: Мир, 1989. — 312 с. — ISBN 5-03-001008-4.
Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. — М., 1956.
Розенфельд Б. А. История неевклидовой геометрии: Развитие понятия о геометрическом пространстве. — М.: Наука, 1976.
Розенфельд Б. А., Юшкевич А. П. Теория параллельных линий на средневековом Востоке. — М.: Наука, 1983.
Смилга В. П. В погоне за красотой. Занимательное введение в неевклидову геометрию. — 2-е изд. — М.: Молодая гвардия, 1988. — 288 с. — (Эврика).
Успенский В. А. Апология математики. Глава 8. Параллельные прямые — в мифологии, реальности и математике. — М.: Амфора, 2009. — ISBN 978-5-367-00689-6.

Спасылкі

Александров А. Д.. Тупость и гений (нявызн.) (недаступная спасылка). «Квант», №№ 11, 12 (1982). Архівавана з першакрыніцы 18 жніўня 2011. Праверана 9 октября 2009.
Возникновение неевклидовой геометрии (нявызн.). Архівавана з першакрыніцы 18 жніўня 2011. Праверана 9 октября 2009.
Пятый постулат Евклида (нявызн.) (недаступная спасылка). Архівавана з першакрыніцы 20 жніўня 2011. Праверана 9 октября 2009.

Тэмы гэтай старонкі (5):
Катэгорыя·Вікіпедыя·Спасылка на Вікісховішча непасрэдна ў артыкуле
Катэгорыя·Еўклідава геаметрыя
Катэгорыя·Планіметрыя
Катэгорыя·Гісторыя матэматыкі
Катэгорыя·Вікіпедыя·Старонкі з модулем Hatnote з чырвонай спасылкай