wd wp Пошук: ⬜

Ступенная функцыя

Ступе́нная, або ступе́невая[1] фу́нкцыя — функцыя выгляду

y

{\displaystyle y=x^{a}}

$\{\displaystyle y=x^\{a\}\}$ , дзе

{\displaystyle a}

$\{\displaystyle a\}$ (паказчык, або паказчык ступені) — некаторы рэчаісны лік [2]. Да ступенных часта прылічваюць і функцыі выгляду

y

{\displaystyle y=kx^{a}}

$\{\displaystyle y=kx^\{a\}\}$ , дзе k — нейкі множнік расцяжэння[3]. Існуе таксама камплекснае абагульненне ступеневай функцыі. На практыцы паказчык ступені амаль заўсёды з’яўляецца цэлым ці рацыянальным лікам.

Рэчаісная ступенная функцыя

Абсяг вызначэння

Калі паказчык ступені — цэлы лік, то ступенную функцыю можна вызначыць на ўсёй лікавай прамой (магчыма, акрамя нуля).
Калі

a

p q

{\displaystyle a={\frac {p}{q}}}

$\{\displaystyle a=\{\frac \{p\}\{q\}\}\}$ , дзе

p , q

{\displaystyle p,q}

$\{\displaystyle p,q\}$ - узаемна простыя лікі,

{\displaystyle q>0}

$\{\displaystyle q>0\}$ - няцотны, то ступенная функцыя таксама вызначана пры любых рэчаісных x (магчыма, акрамя нуля).

У агульным выпадку ступенная функцыя вызначана толькі пры

{\displaystyle x>0}

$\{\displaystyle x>0\}$ (у абсяг вызначэння можа ўваходзіць і нуль, гл. ніжэй).

Калі

{\displaystyle a>0}

$\{\displaystyle a>0\}$ , то функцыя вызначана таксама і пры

x

{\displaystyle x=0}

$\{\displaystyle x=0\}$ .

Пры

a < 0

{\displaystyle a<0}

$\{\displaystyle a<0\}$ нуль ёсць асаблівым пунктам ступеннай функцыі.

Рацыянальны паказчык ступені

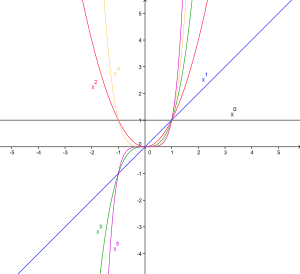
Графікі ступеннай функцыі пры натуральным паказчыку n называюцца парабаламі парадку n. Пры

a

{\displaystyle a=1}

$\{\displaystyle a=1\}$ атрымліваецца лінейная функцыя

y

k x

{\displaystyle y=kx}

$\{\displaystyle y=kx\}$ , называная прамой прапарцыйнай залежнасцю.

Графікі функцый выгляду

y

− n

{\displaystyle y=x^{-n}}

$\{\displaystyle y=x^\{-n\}\}$ , дзе n — натуральны лік, называюцца гіпербаламі парадку n. Пры

a

− 1

{\displaystyle a=-1}

$\{\displaystyle a=-1\}$ атрымліваецца функцыя

y

k x

{\displaystyle y={\frac {k}{x}}}

$\{\displaystyle y=\{\frac \{k\}\{x\}\}\}$ , называная адваротнай прапарцыйнай залежнасцю.

Калі

a

1 n

{\displaystyle a={\frac {1}{n}}}

$\{\displaystyle a=\{\frac \{1\}\{n\}\}\}$ , то функцыя ёсць арыфметычным коранем ступені n.

Прыклад: з трэцяга закону Кеплера вынікае, што перыяд T абарачэння планеты вакол Сонца звязаны з вялікай паўвоссю A яе арбіты наступным чынам:

T

{\displaystyle T=kA^{3/2}}

$\{\displaystyle T=kA^\{3/2\}\}$ (паўкубічная парабала).

Парабалы парадку n:

n

{\displaystyle n=0}

$\{\displaystyle n=0\}$

n

{\displaystyle n=1}

$\{\displaystyle n=1\}$

n

{\displaystyle n=2}

$\{\displaystyle n=2\}$

n

{\displaystyle n=3}

$\{\displaystyle n=3\}$

n

{\displaystyle n=4}

$\{\displaystyle n=4\}$

n

{\displaystyle n=5}

$\{\displaystyle n=5\}$

Гіпербалы парадку n:

n

− 1

{\displaystyle n=-1}

$\{\displaystyle n=-1\}$

n

− 2

{\displaystyle n=-2}

$\{\displaystyle n=-2\}$

n

− 3

{\displaystyle n=-3}

$\{\displaystyle n=-3\}$

Уласцівасці

Гл. таксама: Узвядзенне ў ступень

Функцыя непарыўная і бясконца дыферэнцавальная ва ўсіх кропках, у наваколлі якіх яна вызначана. Нуль, увогуле кажучы, ёсць асаблівым пунктам.

Напрыклад, функцыя

y

{\displaystyle y={\sqrt {x}}}

$\{\displaystyle y=\{\sqrt \{x\}\}\}$ вызначана ў нулі і яго правым наваколлі, але яе вытворная

y

{\displaystyle y={\frac {1}{2{\sqrt {x}}}}}

$\{\displaystyle y=\{\frac \{1\}\{2\{\sqrt \{x\}\}\}\}\}$ у нулі не вызначана.

На прамежку

( 0 , ∞ )

{\displaystyle (0,\infty )}

$\{\displaystyle (0,\infty )\}$ функцыя манатонна нарастае пры

{\displaystyle a>0}

$\{\displaystyle a>0\}$ і манатонна спадае пры

a < 0

{\displaystyle a<0}

$\{\displaystyle a<0\}$ . Значэнні функцыі на гэтым прамежку дадатныя.

Вытворная:

(

)

′

= a

a − 1

{\displaystyle \left(x^{a}\right)^{\prime }=ax^{a-1}}

$\{\displaystyle \left(x^\{a\}\right)^\{\prime \}=ax^\{a-1\}\}$ .

Першаісная:
- Калі
a ≠ − 1

{\displaystyle a\neq -1}

$\{\displaystyle a\neq -1\}$ , то

∫

x

a

d x

x

a + 1

a + 1
C

{\displaystyle \int x^{a},dx={\frac {x^{a+1}}{a+1}}+C}

$\{\displaystyle \int x^\{a\}\,dx=\{\frac \{x^\{a+1\}\}\{a+1\}\}+C\}$
- Калі
a

− 1

{\displaystyle a=-1}

$\{\displaystyle a=-1\}$ , маем

∫

d x

x

= ln ⁡

|

x

|
C

{\displaystyle \int {\frac {dx}{x}}=\ln |x|+C}

$\{\displaystyle \int \{\frac \{dx\}\{x\}\}=\ln |x|+C\}$

Камплексная ступенная функцыя

Асноўны артыкул: Камплексная ступенная функцыя У агульным выпадку ступенная функцыя камплекснай зменнай z азначаецца як[4]:

y

c ⋅ Ln ⁡ ( z )

{\displaystyle y=z^{c}=e^{c\cdot \operatorname {Ln} (z)}}

$\{\displaystyle y=z^\{c\}=e^\{c\cdot \operatorname \{Ln\} (z)\}\}$ Тут паказчык ступені c — некаторы камплексны лік. Значэнне функцыі, адпаведнае галоўнаму значэнню лагарыфму, называецца галоўным значэннем ступені. Напрыклад, значэнне

{\displaystyle i^{i}}

$\{\displaystyle i^\{i\}\}$ роўнае

− ( 4 k + 1 )

π 2

{\displaystyle e^{-(4k+1){\frac {\pi }{2}}}}

$\{\displaystyle e^\{-(4k+1)\{\frac \{\pi \}\{2\}\}\}\}$ , дзе k — адвольны цэлы, а яго галоўнае значэнне роўнае

i ln ⁡ ( i )

−

π 2

{\displaystyle e^{i\ln(i)}=e^{-{\frac {\pi }{2}}}}

$\{\displaystyle e^\{i\ln(i)\}=e^\{-\{\frac \{\pi \}\{2\}\}\}\}$ .

Камплексная ступенная функцыя істотна адрозніваецца ад свайго рэчаіснага адменніку. З-за мнагазначнасці камплекснага лагарыфму яна, увогуле кажучы, таксама мае бясконца многа значэнняў. Аднак два выпадкі, важныя ў прыкладаннях, разглядаюцца асобна:

Пры натуральным паказчыку ступені функцыя

y

{\displaystyle y=z^{n}}

$\{\displaystyle y=z^\{n\}\}$ адназначная і n-лістная [5]. 2. Калі паказчык ступені — дадатны рацыянальны лік, г.зн. (нескарачальны) дроб

p q

{\displaystyle {\frac {p}{q}}}

$\{\displaystyle \{\frac \{p\}\{q\}\}\}$ , то функцыя будзе мець q розных значэнняў[4].

Крыніцы

↑
Матэматычная энцыклапедыя. Гал. рэд. В. Бернік. Мн.: Тэхналогія, 2001. с. 330.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, §48: Важнейшие классы функций.
↑
Выгодский М. Я. Справочник по элементарной математике. М.: Наука,1978. Стр. 312.
1 2 Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 526-527.
↑
Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.

Літаратура

Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5. — С. 208-209.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — изд. 6-е. — М.: Наука, 1966.

Гл. таксама

Спасылкі

Ступенная функцыя

Тэмы гэтай старонкі (2):
Катэгорыя·Вікіпедыя·Старонкі з модулем Hatnote з чырвонай спасылкай
Катэгорыя·Элементарныя функцыі