wd wp Пошук: ⬜

Адзінкавая акружнасць

Адзі́нкавая акру́жнасць — акружнасць з радыусам 1 і цэнтрам у пачатку каардынат.

Для каардынат (x, y) усіх пунктаў на адзінкавай акружнасці, згодна з тэарэмай Піфагора, выконваецца роўнасць:

x

2

y

2

= 1.

{\displaystyle x^{2}+y^{2}=1.}

Паняцце адзінкавай акружнасці абагульняецца да n-мернай прасторы (

n

2

{\displaystyle n>2}

), у такім выпадку кажуць аб «адзінкавай сферы».

Трыганаметрычныя функцыі

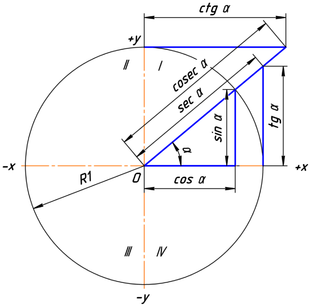
З дапамогай адзінкавай акружнасці могуць быць наглядна апісаны трыганаметрычныя функцыі.

Сінус і косінус могуць быць апісаны наступным чынам: калі злучыць любую кропку

( x , y )

{\displaystyle (x,y)}

на адзінкавай акружнасці з пачаткам каардынат

( 0 , 0 )

{\displaystyle (0,0)}

, атрымліваецца адрэзак, які знаходзіцца пад вуглом

α

{\displaystyle \alpha }

адносна дадатнай паўвосі абсцыс. Тады сапраўды:

cos ⁡ α

x ,

{\displaystyle \cos \alpha =x,}

sin ⁡ α

y .

{\displaystyle \sin \alpha =y.}

Пры падстаноўцы гэтых значэнняў ва ўраўненне акружнасці

x

2

y

2

= 1

{\displaystyle x^{2}+y^{2}=1}

атрымліваецца:

cos

2

⁡ α +

sin

2

⁡ α

{\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1.}

(Выкарыстоўваецца наступнае агульнапрынятае абазначэнне:

cos

2

⁡ x

( cos ⁡ x

)

2

{\displaystyle \cos ^{2}x=(\cos x)^{2}}

.)

Тут жа наглядна апісваецца перыядычнасць трыганаметрычных функцый, бо адпаведнае вуглу становішча адрэзка не залежыць ад колькасці «поўных абаротаў»:

sin ⁡ ( x + 2 π k )

sin ⁡ ( x )

{\displaystyle \sin(x+2\pi k)=\sin(x)}

cos ⁡ ( x + 2 π k )

cos ⁡ ( x )

{\displaystyle \cos(x+2\pi k)=\cos(x)}

для ўсіх цэлых лікаў

k

{\displaystyle k}

, г.зн. для

k ∈

Z

{\displaystyle k\in \mathbb {Z} }

.

Камплексная плоскасць

Гл. таксама: Формула Эйлера і U(1) На камплекснай плоскасці адзінкавая акружнасць — гэта наступнае мноства

G ⊂

C

{\displaystyle G\subset \mathbb {C} }

:

G

{ z :

|

z

|

= 1 }

{

e

i ϕ

: 0 ≤ ϕ < 2 π } .

{\displaystyle G=\{z:|z|=1\}=\{e^{i\phi }:0\leq \phi <2\pi \}.}

Мноства

G

{\displaystyle G}

з’яўляецца падгрупай групы камплексных лікаў па множанню, яе нейтральны элемент — гэта

e

i 0

= 1

{\displaystyle e^{i0}=1}

.

Гл. таксама

• Адзінкавая сфера
• Адзінкавы круг
• Адзінкавы квадрат
• Адзінкавы куб

Тэмы гэтай старонкі (3):
Катэгорыя·Геаметрычныя фігуры
Катэгорыя·Вікіпедыя·Старонкі з модулем Hatnote з чырвонай спасылкай
Катэгорыя·Трыганаметрыя