wd wp Пошук: ⬜

Частковая вытворная

У гэтага паняцця ёсць і іншыя значэнні, гл. Вытворная. У матэматычным аналізе частковая вытворная — адно з абагульненняў паняцця вытворнай на выпадак функцыі некалькіх зменных.

У яўным выглядзе частковая вытворная функцыі

f

{\displaystyle f}

у кропцы

(

a

1

,

a

2

, … ,

a

n

)

{\displaystyle (a_{1},a_{2},\ldots ,a_{n})}

вызначаецца наступным чынам:

∂ f

∂

x

k

(

a

1

, ⋯ ,

a

n

)

lim

Δ x → 0

f (

a

1

, … ,

a

k

Δ x , … ,

a

n

) − f (

a

1

, … ,

a

k

, … ,

a

n

)

Δ x

.

{\displaystyle {\frac {\partial f}{\partial x_{k}}}(a_{1},\cdots ,a_{n})=\lim _{\Delta x\to 0}{\frac {f(a_{1},\ldots ,a_{k}+\Delta x,\ldots ,a_{n})-f(a_{1},\ldots ,a_{k},\ldots ,a_{n})}{\Delta x}}.}

Абазначэнне

Варта звярнуць увагу, што абазначэнне

∂ f

∂ x

{\displaystyle {\frac {\partial f}{\partial x}}}

трэба разумець як цэльны сімвал, у адрозненне ад звычайнай вытворнай функцыі адной зменнай

d f

d x

,

{\displaystyle {\frac {df}{dx}},}

якую можна прадставіць, як адносіну дыферэнцыялаў функцыі і аргумента. Аднак, і частковую вытворную можна прадставіць як адносіну дыферэнцыялаў, але ў гэтым выпадку неабходна абавязкова паказваць, па якой зменнай ажыццяўляецца прырашчэнне функцыі:

∂ f

∂ x

=

d

x

f

d x

,

{\displaystyle {\frac {\partial f}{\partial x}}={\frac {d_{x}f}{dx}},}

дзе

d

x

f

{\displaystyle d_{x}f}

— частковы дыферэнцыял функцыі

f

{\displaystyle f}

па зменнай

x

{\displaystyle x}

. Часта неразуменне факта цэльнасці сімвала

∂ f

∂ x

{\displaystyle {\frac {\partial f}{\partial x}}}

з’яўляецца прычынай памылак і непаразуменняў, як, напрыклад, скарачэнне

∂ x

{\displaystyle \partial x}

ў выразе

∂ f

∂ x

∂ x

∂ t

{\displaystyle {\frac {\partial f}{\partial x}}{\frac {\partial x}{\partial t}}}

[1].

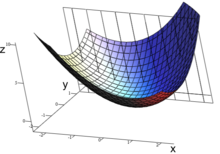
Геаметрычная інтэрпрэтацыя

Геаметрычна частковая вытворная з’яўляецца вытворнай па напрамку адной з каардынатных восей. Частковая вытворная функцыі

f

{\displaystyle f}

у пункце

x →

0

= (

x

1

0

, … ,

x

n

0

)

{\displaystyle {\vec {x}}{,}^{0}=(x_{1}^{0},\ldots ,x_{n}^{0})}

па каардынаце

x

k

{\displaystyle x_{k}}

роўная вытворнай

∂ f

∂

e →

{\displaystyle {\frac {\partial f}{\partial {\vec {e}}}}}

па напрамку

e →

=

e →

k

= ( 0 , … , 0 , 1 , 0 , … , 0 )

{\displaystyle {\vec {e}}={\vec {e}}{,}^{k}=(0,\ldots ,0,1,0,\ldots ,0)}

, дзе адзінка стаіць на k-ым месцы.

Прыклады

Аб’ём V конуса залежыць ад вышыні h і радыуса r, згодна з формулай

V

π

r

2

h

3

,

{\displaystyle V={\frac {\pi r^{2}h}{3}},}

Частковая вытворная аб’ёму V адносна радыуса r

∂ V

∂ r

=

2 π r h

3

,

{\displaystyle {\frac {\partial V}{\partial r}}={\frac {2\pi rh}{3}},}

якая паказвае хуткасць, з якой змяняецца аб’ём конуса, калі яго радыус мяняецца, а яго вышыня застаецца нязменнай. Напрыклад, калі лічыць адзінкі вымярэння аб’ёму

m

3

{\displaystyle m^{3}}

, а вымярэнні даўжыні

m

{\displaystyle m}

, то вышэйназваная вытворная будзе мець размернасць хуткасці змянення аб’ёму

m

3

/

m

{\displaystyle m^{3}/m}

, г.зн. змяненне велічыні радыуса на 1 м будзе адпавядаць змяненню аб’ёму конуса на

2 π r h

3

{\displaystyle {\frac {2\pi rh}{3}}}

m

3

{\displaystyle m^{3}}

.

Частковая вытворная адносна h

∂ V

∂ h

=

π

r

2

3

,

{\displaystyle {\frac {\partial V}{\partial h}}={\frac {\pi r^{2}}{3}},}

якая паказвае хуткасць, з якой змяняецца аб’ём конуса, калі яго вышыня мяняецца, а яго радыус застаецца нязменным.

Поўная вытворная V адносна r і h

d ⁡ V

d ⁡ r

=

2 π r h

3

⏞

∂ V

∂ r

π

r

2

3

⏞

∂ V

∂ h

d ⁡ h

d ⁡ r

{\displaystyle {\frac {\operatorname {d} V}{\operatorname {d} r}}=\overbrace {\frac {2\pi rh}{3}} ^{\frac {\partial V}{\partial r}}+\overbrace {\frac {\pi r^{2}}{3}} ^{\frac {\partial V}{\partial h}}{\frac {\operatorname {d} h}{\operatorname {d} r}}}

і

d ⁡ V

d ⁡ h

=

π

r

2

3

⏞

∂ V

∂ h

2 π r h

3

⏞

∂ V

∂ r

d ⁡ r

d ⁡ h

{\displaystyle {\frac {\operatorname {d} V}{\operatorname {d} h}}=\overbrace {\frac {\pi r^{2}}{3}} ^{\frac {\partial V}{\partial h}}+\overbrace {\frac {2\pi rh}{3}} ^{\frac {\partial V}{\partial r}}{\frac {\operatorname {d} r}{\operatorname {d} h}}}

Адрозненне паміж поўнай і частковай вытворнай — ухіленне ўскосных залежнасцей паміж зменнымі ў апошняй.

Калі (па некаторых прычынах) прапорцыі конуса застаюцца нязменнымі, то вышыня і радыус знаходзяцца ў фіксаванай адносіне s,

s

h r

=

d ⁡ h

d ⁡ r

.

{\displaystyle s={\frac {h}{r}}={\frac {\operatorname {d} h}{\operatorname {d} r}}.}

Гэта дае поўную вытворную адносна r:

d ⁡ V

d ⁡ r

=

2 π r h

3

s

π

r

2

3

{\displaystyle {\frac {\operatorname {d} V}{\operatorname {d} r}}={\frac {2\pi rh}{3}}+s{\frac {\pi r^{2}}{3}}}

Ураўненні, у якія ўваходзяць частковыя вытворныя, называюцца дыферэнцыяльнымі ўраўненнямі ў частковых вытворных і шырока вядомыя ў фізіцы, інжынерыі і іншых навуках і прыкладных дысцыплінах.

Зноскі

1. ↑ Фихтенгольц, «Курс дифференциального и интегрального исчисления»

Тэмы гэтай старонкі (2):
Катэгорыя·Дыферэнцыяльнае злічэнне
Катэгорыя·Іншыя значэнні: старонка не існуе