wd wp Пошук: ⬜

Гама-функцыя

Гама-функцыя (або Эйлераў інтэграл другога роду) — матэматычная функцыя, якая пашырае паняцце фактарыяла на поле камплексных лікаў. Звычайна абазначаецца грэчаскай літарай гама Γ(z).

Для натуральных n справядліва роўнасць:

Γ ( n )

( n − 1 ) !

{\displaystyle \Gamma (n)=(n-1)!}

$\{\displaystyle \Gamma (n)=(n-1)!\}$ Гама-функцыя вызначана для ўсіх камплексных лікаў, за выключэннем адмоўных цэлых і нуля. Для камплексных лікаў з дадатнай рэчаіснай часткай, функцыя вызначаецца з дапамогаю збежнага неўласцівага інтэграла:

Γ ( t )

∫

∞

t − 1

− x

d x .

{\displaystyle \Gamma (t)=\int \limits _{0}^{\infty }x^{t-1}e^{-x},dx.}

$\{\displaystyle \Gamma (t)=\int \limits _\{0\}^\{\infty \}x^\{t-1\}e^\{-x\}\,dx.\}$ Гэту інтэгральную функцыю можна аналітычна працягнуць на ўсю камплексную плоскасць, за выключэннем недадатных цэлых лікаў (дзе функцыя мае простыя полюсы). Атрыманая ў выніку мераморфная функцыя і называецца гама-функцыяй.

Была ўведзена Леанардам Эйлерам, а сваім абазначэннем гама-функцыя абавязана Лежандру.

Азначэнні

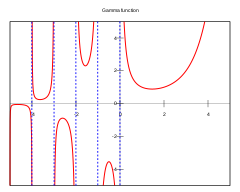
Інтэгральнае азначэнне

Калі рэчаісная частка камплекснага ліку

{\displaystyle z}

$\{\displaystyle z\}$ дадатная, то Гама-функцыя вызначаецца праз інтэграл

Γ ( z )

∫

∞

− 1

− t

d t ,

z ∈

R e

( z )

{\displaystyle ~\Gamma (z)=\int \limits _{0}^{+\infty }t^{{\mathrm {z} }-1}e^{-t},dt,\quad z\in \mathbb {C} :\mathrm {Re} (z)>0}

$\{\displaystyle ~\Gamma (z)=\int \limits _\{0\}^\{+\infty \}t^\{\{\mathrm \{z\} \}-1\}e^\{-t\}\,dt,\quad z\in \mathbb \{C\} :\mathrm \{Re\} (z)>0\}$ На ўсю камплексную плоскасць функцыя аналітычна працягваецца праз тоеснасць

Γ ( z + 1 )

z Γ ( z ) .

{\displaystyle ~\Gamma (z+1)=z\Gamma (z).}

$\{\displaystyle ~\Gamma (z+1)=z\Gamma (z).\}$ Існуе непасрэдны аналітычны працяг зыходнай формулы на ўсю камплексную плоскасць, т. зв. інтэграл Рымана-Ханкеля

Γ ( z )

i 2 π

− 1

∫

− 1

− t

d t ,

z ∈

∖ { 0 , − 1 , − 2 , … } .

{\displaystyle ~\Gamma (z)={\frac {1}{e^{i2\pi {\mathrm {z} }}-1}}\int \limits _{L}!t^{{\mathrm {z} }-1}e^{-t},dt,\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \}.}

$\{\displaystyle ~\Gamma (z)=\{\frac \{1\}\{e^\{i2\pi \{\mathrm \{z\} \}\}-1\}\}\int \limits _\{L\}\!t^\{\{\mathrm \{z\} \}-1\}e^\{-t\}\,dt,\quad z\in \mathbb \{C\} \setminus \\{0,-1,-2,\ldots \\}.\}$ дзе контур

{\displaystyle L}

$\{\displaystyle L\}$ — любы контур на камплекснай плоскасці, які абходзіць пункт

t

{\displaystyle t=0}

$\{\displaystyle t=0\}$ супраць гадзіннікавай стрэлкі, і канцы якога ідуць на бесканечнасць уздоўж дадатнай рэчаіснае восі.

Наступныя выразы з’яўляюцца альтэрнатыўнымі азначэннямі Гама-функцыі.

Азначэнне па Гаусу

Яно вернае для ўсіх камплексных

{\displaystyle z}

$\{\displaystyle z\}$ , за выключэннем 0 і адмоўных цэлых лікаў

Γ ( z )

lim

n → ∞

n !

z ( z + 1 ) ( z + 2 ) ⋯ ( z + n )

z ∈

∖ { 0 , − 1 , − 2 , … } .

{\displaystyle \Gamma (z)=\lim \limits _{n\to \infty }{\frac {n!,n^{z}}{z(z+1)(z+2)\cdots (z+n)}},\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \}.}

$\{\displaystyle \Gamma (z)=\lim \limits _\{n\to \infty \}\{\frac \{n!\,n^\{z\}\}\{z(z+1)(z+2)\cdots (z+n)\}\},\quad z\in \mathbb \{C\} \setminus \\{0,-1,-2,\ldots \\}.\}$

Азначэнне па Эйлеру

Γ ( z )

1 z

(

∏

n

∞

(

1 +

1 n

)

(

1 +

z n

)

− 1

)

1 z

∏

n

∞

(

1 +

1 n

)

1 +

z ∈

∖ { 0 , − 1 , − 2 , … } .

{\displaystyle \Gamma (z)={\frac {1}{z}}\left(\prod \limits _{n=1}^{\infty }{\left(1+{\frac {1}{n}}\right)}^{z}{\left(1+{\frac {z}{n}}\right)}^{-1}\right)={\frac {1}{z}}\prod _{n=1}^{\infty }{\frac {\left(1+{\frac {1}{n}}\right)^{\mathrm {z} }}{1+{\frac {\mathrm {z} }{n}}}},\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \}.}

$\{\displaystyle \Gamma (z)=\{\frac \{1\}\{z\}\}\left(\prod \limits _\{n=1\}^\{\infty \}\{\left(1+\{\frac \{1\}\{n\}\}\right)\}^\{z\}\{\left(1+\{\frac \{z\}\{n\}\}\right)\}^\{-1\}\right)=\{\frac \{1\}\{z\}\}\prod _\{n=1\}^\{\infty \}\{\frac \{\left(1+\{\frac \{1\}\{n\}\}\right)^\{\mathrm \{z\} \}\}\{1+\{\frac \{\mathrm \{z\} \}\{n\}\}\}\},\quad z\in \mathbb \{C\} \setminus \\{0,-1,-2,\ldots \\}.\}$

Азначэнне па Веерштрасу

Γ ( z )

− γ z

∏

n

∞

(

1 +

z n

)

− 1

z ∈

∖ { 0 , − 1 , − 2 , … } ,

{\displaystyle \Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n},\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \},}

$\{\displaystyle \Gamma (z)=\{\frac \{e^\{-\gamma z\}\}\{z\}\}\prod _\{n=1\}^\{\infty \}\left(1+\{\frac \{z\}\{n\}\}\right)^\{-1\}e^\{z/n\},\quad z\in \mathbb \{C\} \setminus \\{0,-1,-2,\ldots \\},\}$ дзе

γ

lim

n → ∞

(

∑

k

1 k

− ln ⁡

)

≈ 0 , 57722

{\displaystyle \gamma =\lim \limits _{n\to \infty }\left(\sum \limits _{k=1}^{n}{\frac {1}{k}}-\ln {n}\right)\approx 0,57722}

$\{\displaystyle \gamma =\lim \limits _\{n\to \infty \}\left(\sum \limits _\{k=1\}^\{n\}\{\frac \{1\}\{k\}\}-\ln \{n\}\right)\approx 0,57722\}$ — пастаянная Эйлера — Маскероні.

Заўвагі

Вышэйпрыведзены інтэграл збягаецца абсалютна, калі рэчаісная частка камплекснага ліку

{\displaystyle z}

$\{\displaystyle z\}$ дадатна.

Прымяняючы інтэграванне па частках, можна паказаць, што тоеснасць

Γ ( z + 1 )

z Γ ( z )

{\displaystyle \Gamma (z+1)=z\Gamma (z)}

$\{\displaystyle \Gamma (z+1)=z\Gamma (z)\}$

справядліва для падынтэгральнага выразу.

Паколькі

Γ ( 1 )

{\displaystyle \Gamma (1)=1}

$\{\displaystyle \Gamma (1)=1\}$ , для ўсіх натуральных лікаў

{\displaystyle n}

$\{\displaystyle n\}$

Γ ( n + 1 )

n ⋅ Γ ( n )

…

n ! ⋅ Γ ( 1 )

n !

{\displaystyle \Gamma (n+1)=n\cdot \Gamma (n)=\ldots =n!\cdot \Gamma (1)=n!}

$\{\displaystyle \Gamma (n+1)=n\cdot \Gamma (n)=\ldots =n!\cdot \Gamma (1)=n!\}$

Γ ( z )

{\displaystyle \Gamma (z)}

$\{\displaystyle \Gamma (z)\}$ з’яўляецца мераморфнаю на камплекснай плоскасці і мае полюсы ў пунктах

z

0 ,

− 1 ,

− 2 ,

− 3 ,

…

{\displaystyle z=0,;-1,;-2,;-3,;\ldots }

$\{\displaystyle z=0,\;-1,\;-2,\;-3,\;\ldots \}$

Звязаныя азначэнні

Калі-нікалі выкарыстоўваецца альтэрнатыўны запіс, так званая пі-функцыя, якая звязана з гама-функцыяй наступным чынам:

Π ( z )

Γ ( z + 1 )

z Γ ( z ) .

{\displaystyle \Pi (z)=\Gamma (z+1)=z\Gamma (z).}

$\{\displaystyle \Pi (z)=\Gamma (z+1)=z\Gamma (z).\}$

У інтэграле з азначэння гама-функцыі, межы інтэгравання нязменныя. Разглядаюць таксама няпоўную гама-функцыю, якую вызначаюць падобным інтэгралам са зменнай верхняй ці ніжняй мяжою інтэгравання. Вылучаюць верхнюю няпоўную гама-функцыю, якую часта абазначаюць як гама-функцыю ад двух аргументаў:

Γ ( a , z )

∫

∞

a − 1

− t

d t

{\displaystyle \Gamma (a,z)=\int \limits _{\mathrm {z} }^{\infty }{t^{a-1}e^{-t},dt},}

$\{\displaystyle \Gamma (a,z)=\int \limits _\{\mathrm \{z\} \}^\{\infty \}\{t^\{a-1\}e^\{-t\}\,dt\},\}$ і ніжнюю няпоўную гама-функцыю, якую таксама абазначаюць малой літарай «гама»:

γ ( a , z )

∫

a − 1

− t

d t

{\displaystyle \gamma (a,z)=\int \limits _{0}^{\mathrm {z} }{t^{a-1}e^{-t},dt}.}

$\{\displaystyle \gamma (a,z)=\int \limits _\{0\}^\{\mathrm \{z\} \}\{t^\{a-1\}e^\{-t\}\,dt\}.\}$ Уласцівасці

Формула дапаўнення Эйлера:

Γ ( 1 − z ) Γ ( z )

sin ⁡ π z

{\displaystyle \Gamma (1-z)\Gamma (z)={\pi \over \sin \pi z}.}

$\{\displaystyle \Gamma (1-z)\Gamma (z)=\{\pi \over \sin \pi z\}.\}$

З яе вынікае формула памнажэння Гауса been:

Γ ( z ) Γ

(

z +

1 n

)

… Γ

(

z +

n − 1

)

1 2

− n z

⋅ ( 2 π

)

n − 1

Γ ( n z ) ,

{\displaystyle \Gamma (z)\Gamma \left(z+{\frac {1}{n}}\right)\ldots \Gamma \left(z+{\frac {n-1}{n}}\right)=n^{{\frac {1}{2}}-nz}\cdot (2\pi )^{\frac {n-1}{2}}\Gamma (nz),}

$\{\displaystyle \Gamma (z)\Gamma \left(z+\{\frac \{1\}\{n\}\}\right)\ldots \Gamma \left(z+\{\frac \{n-1\}\{n\}\}\right)=n^\{\{\frac \{1\}\{2\}\}-nz\}\cdot (2\pi )^\{\frac \{n-1\}\{2\}\}\Gamma (nz),\}$

якую пры n=2 называюць формулай падваення Лежандра:

Γ ( z )

(

z +

1 2

)

1 − 2 z

Γ ( 2 z ) .

{\displaystyle \Gamma (z);\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z};{\sqrt {\pi }};\Gamma (2z).,!}

$\{\displaystyle \Gamma (z)\;\Gamma \left(z+\{\frac \{1\}\{2\}\}\right)=2^\{1-2z\}\;\{\sqrt \{\pi \}\}\;\Gamma (2z).\,\!\}$

Гама-функцыя мае полюс у

z

− n

{\displaystyle z=-n}

$\{\displaystyle z=-n\}$ для любога натуральнага

{\displaystyle n}

$\{\displaystyle n\}$ і нуля; вылік у гэтым пункце задаецца так:

Res

z

− n

⁡ Γ ( z )

( − 1

)

n !

{\displaystyle \operatorname {Res} _{z=-n}\Gamma (z)={\frac {(-1)^{n}}{n!}}.}

$\{\displaystyle \operatorname \{Res\} _\{z=-n\}\Gamma (z)=\{\frac \{(-1)^\{n\}\}\{n!\}\}.\}$

Наступнае прадстаўленне гама-функцыі ў выглядзе бесканечнага здабытку, як паказаў Веерштрас, верна для ўсіх камплексных

{\displaystyle z}

$\{\displaystyle z\}$ , акрамя недадатных цэлых лікаў:

Γ ( z )

− γ z

∏

k

∞

(

1 +

z k

)

− 1

{\displaystyle \Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{k=1}^{\infty }\left(1+{\frac {z}{k}}\right)^{-1}e^{z/k},}

$\{\displaystyle \Gamma (z)=\{\frac \{e^\{-\gamma z\}\}\{z\}\}\prod _\{k=1\}^\{\infty \}\left(1+\{\frac \{z\}\{k\}\}\right)^\{-1\}e^\{z/k\},\}$

дзе

{\displaystyle \gamma }

$\{\displaystyle \gamma \}$ — пастаянная Эйлера — Маскероні.

Важная ўласцівасць, якая вынікае з гранічнага азначэння:

Γ ( z )

= Γ (

z ¯

)

{\displaystyle {\overline {\Gamma (z)}}=\Gamma ({\overline {z}})}

$\{\displaystyle \{\overline \{\Gamma (z)\}\}=\Gamma (\{\overline \{z\}\})\}$ .

Гама-функцыя бесканечна дыферэнцавальная, і

′

( x )

ψ ( x ) Γ ( x ) ,

{\displaystyle \Gamma ^{\prime }(x)=\psi (x)\Gamma (x),}

$\{\displaystyle \Gamma ^\{\prime \}(x)=\psi (x)\Gamma (x),\}$

дзе

ψ ( x )

{\displaystyle \psi (x)}

$\{\displaystyle \psi (x)\}$ часта называюць «псі-функцыяй», ці дыгама-функцыяй.

Гама-функцыя і бэта-функцыя звязаны наступнымі суадносінамі:

( x , y )

Γ ( x ) Γ ( y )

Γ ( x + y )

{\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}}.}

$\{\displaystyle \mathrm \{B\} (x,y)=\{\frac \{\Gamma (x)\Gamma (y)\}\{\Gamma (x+y)\}\}.\}$

Асобныя значэнні

Найбольш вядомыя значэнні гама-функцыі ад няцэлага аргумента:

(

1 2

)

{\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}.}

$\{\displaystyle \Gamma \left(\{\frac \{1\}\{2\}\}\right)=\{\sqrt \{\pi \}\}.\}$

(

1 4

)

( 2 π

)

A G M (

, 1 )

{\displaystyle \Gamma \left({\frac {1}{4}}\right)={\sqrt {\frac {(2\pi )^{3/2}}{AGM({\sqrt {2}},1)}}},}

$\{\displaystyle \Gamma \left(\{\frac \{1\}\{4\}\}\right)=\{\sqrt \{\frac \{(2\pi )^\{3/2\}\}\{AGM(\{\sqrt \{2\}\},1)\}\}\},\}$ дзе AGM(x, y) — сярэдняе арыфметыка-геаметрычнае(англ.) бел. лікаў x і y.

(

3 2

)

{\displaystyle \Gamma \left({\frac {3}{2}}\right)={\frac {\sqrt {\pi }}{2}}.}

$\{\displaystyle \Gamma \left(\{\frac \{3\}\{2\}\}\right)=\{\frac \{\sqrt \{\pi \}\}\{2\}\}.\}$

(

1 2

)

( 2 n ) !

n !

( 2 n − 1 ) ! !

⋅

[

(

n −

1 2

)

n !

]

{\displaystyle \Gamma \left({\frac {1}{2}}+n\right)={(2n)! \over 4^{n}n!}{\sqrt {\pi }}={\frac {(2n-1)!!}{2^{n}}},{\sqrt {\pi }}={\sqrt {\pi }}\cdot \left[{n-{\frac {1}{2}} \choose n}n!\right]}

$\{\displaystyle \Gamma \left(\{\frac \{1\}\{2\}\}+n\right)=\{(2n)! \over 4^\{n\}n!\}\{\sqrt \{\pi \}\}=\{\frac \{(2n-1)!!\}\{2^\{n\}\}\}\,\{\sqrt \{\pi \}\}=\{\sqrt \{\pi \}\}\cdot \left[\{n-\{\frac \{1\}\{2\}\} \choose n\}n!\right]\}$

(

1 2

− n

)

( − 4

)

n !

( 2 n ) !

( − 2

)

( 2 n − 1 ) ! !

[

(

−

1 2

)

n !

]

{\displaystyle \Gamma \left({\frac {1}{2}}-n\right)={(-4)^{n}n! \over (2n)!}{\sqrt {\pi }}={\frac {(-2)^{n}}{(2n-1)!!}},{\sqrt {\pi }}={\sqrt {\pi }}/\left[{-{\frac {1}{2}} \choose n}n!\right]}

$\{\displaystyle \Gamma \left(\{\frac \{1\}\{2\}\}-n\right)=\{(-4)^\{n\}n! \over (2n)!\}\{\sqrt \{\pi \}\}=\{\frac \{(-2)^\{n\}\}\{(2n-1)!!\}\}\,\{\sqrt \{\pi \}\}=\{\sqrt \{\pi \}\}/\left[\{-\{\frac \{1\}\{2\}\} \choose n\}n!\right]\}$

Гл. таксама

Літаратура

Купцов Л. П. Гамма-функция // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия. — Т. 1.

Спасылкі

Weisstein, Eric W. Gamma Function(англ.) на старонцы Wolfram MathWorld.

Тэмы гэтай старонкі (1):
Катэгорыя·Спецыяльныя функцыі